Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 44

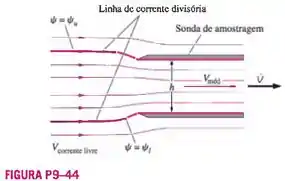
No controle de poluição do ar, precisa-se frequentemente medir a qualidade de uma corrente de ar em movimento. Nessas medições, uma sonda de amostragem é alinhada com o escoamento do ar conforme mostra a Figura P9-44. Uma bomba de sucção extrai o ar através da sonda a uma vazão em volume V ˙ conforme mostra a figura. Para uma amostragem precisa, a velocidade do ar através da sonda deverá ser a mesma da corrente de ar (amostragem isocinética). Porém, se a sucção aplicada for muito forte, como está ilustrado na Figura P9-44, a velocidade do ar através da sonda é maior do que aquela da corrente de ar (amostragem superisocinética). Para simplificar considere um caso no qual a altura da sonda de amostragem é h   =   4,5   m m e sua largura (para dentro da página da Figura P9-44) é W = 52   m m . Os valores da função corrente correspondentes às linhas de corrente divisórias superior e inferior são ψ l = 0,105   m 2 / s e ψ u = 0,150   m 2 / s , respectivamente. Calcule a vazão em volume através da sonda (em unidades de m 3 / s ) e a velocidade média do ar sugado pela sonda.

Passo 1

E aí, galera? Como estão os estudos? Vamos fazer uma quertão de função corrente ψ ?

Pessoal, o enunciado quer que a gente calcule a vazão em volume V ˙ através de uma sonda e a velocidademédia V m é d através da sonda. Para fazer essas contas, a questão nos informa os dados mostrados na figura abaixo.

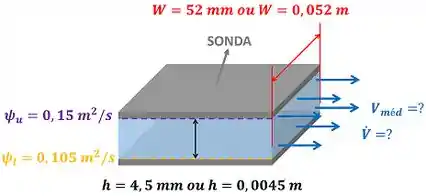
onde h é a distância entre as placas que formam a sonda, W é a largura da sonda, ψ u é a função corrente do fluido que está em contato com a placa de cima e ψ l é a função corrente do fluido que está em contato com a placa de baixo.

Com essas informações, podemos entender como calcular V ˙ no próximo passo.

Passo 2

Para calcular a vazão volumétrica V ˙ a partir dos valores de duas funções corrente, temos que utilizar a equação 9-25 do livro. Ela diz que a vazão por unidade de largura V ˙ / W que passa através de duas linhas de corrente com valores ψ u (para a linha de cima) e ψ l (para a linha de baixo) pode ser calculada com a fórmula abaixo.

V ˙ W = ψ u - ψ l

Passando W para o outro lado da equação, achamos uma equação para V ˙ .

V ˙ = ψ u - ψ l ⋅ W

Substituindo os valores dos dados, V ˙ pode ser calculada.

V ˙ = ψ u - ψ l ⋅ W       ⟹       V ˙ = 0,15 - 0,105 ⋅ 0,052       ⟹       V ˙ = 0 , 00234   m 3 / s

Passo 3

A partir desse valor de vazão volumétrica V ˙ , achamos V m é d a partir da equação abaixo. Vemos que basta dividir a vazão pela área A A = W ⋅ h pela qual o fluido passa para obter V m é d .

V m é d = V ˙ A     ⟹     V m é d = V ˙ W ⋅ h     ⟹     V m é d = 0 , 00234 0,052 ⋅ 0,0045       ⟹       V m é d = 10   m / s

Resposta

V ˙ = 0 , 00234   m 3 / s

V m é d = 10   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O teorema do divergente é expresso como: ∫ V ∇ →. G → d V = ∮ A G →. n → d A onde G → é um vetor, V é um volume e A é a área da superfície que delimita e define o volume. Expresse o teorema do diverge
Uma expansão em séries de Taylor da função f ( x ) ao redor de alguma posição x 0 é dada por: f x 0 + d x = f x 0 + d f d x x = x 0 d x + 1 2 ! d 2 f d x 2 x = x 0 d x 2 + 1 3 ! d 3 f d x 3 x = x 0 d
Use a regra do produto do Problema 9-11 para demonstrar que ∇ → . ρ V → V → = V → ∇ →. ρ V → + ρ ( V→. ∇ → ) V → .
Transforme a posição x → =( 4 ,3 , -4 ) de coordenadas cartesianas ( x ,y ,z ) em coordenadas cilíndricas ( r ,θ ,z ) , incluindo as unidades. Os valores de x → estão em unidades de metros.
Deixe o vetor G → ser dado por G → = 2 x z i → - 1 2 x 2 j → + z 2 k → . Calcule o divergente de G → , e simplifique o máximo possível. Existe algo de especial no seu resultado?