Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 47
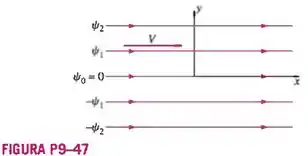
Considere um campo de escoamento permanente, bidimensional, incompressível chamado de corrente uniforme. A velocidade do fluido é em qualquer ponto, e o escoamento é alinhado com o eixo (Figura P9-47). As componentes cartesianas da velocidade são e . Encontre uma expressão para a função corrente para esse escoamento. Suponha . Se for uma reta horizontal em e o valor de ao longo do eixo for zero, calcule a vazão em volume por unidade de largura (para dentro da página da Figura P9-47) entre essas duas linhas de corrente.
Passo 1
Essa é uma questão de função corrente! O enunciado dela quer saber duas informações: uma expressão para a função corrente desse escoamento e o valor da vazão volumétrica por unidade de largura que passa entre as linhas de corrente com funções correntes que valem e . A figura abaixo mostra os dados que temos e as informações que buscamos.
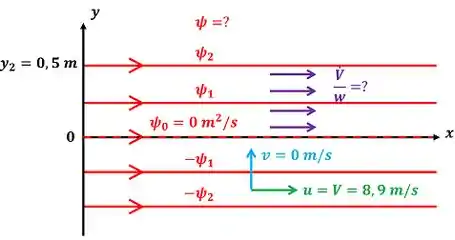
onde é a função corrente do escoamento, é o valor da função corrente da linha de corrente que se encontra em , é o valor da função corrente da linha de corrente que se encontra em , é o valor da função corrente da linha de corrente que se encontra em . é a componente vertical da velocidade do fluido, é a componente horizontal da velocidade do fluido (que vale ).
Depois de entender todos esses dados, podemos entender como encontrar uma expressão para a partir das velocidade e .
Passo 2
Para descobrir as fórmulas das componentes da velocidade no eixo e no eixo , derivamos parcialmente a função corrente . E como fazemos o inverso? Ou seja, como descobrimos uma fórmula para a função corrente a partir das componentes da velocidade ( e )?
Para fazer esse caminho inverso, usamos o inverso da derivada: a integral! Em outras palavras, descobrimos uma fórmula para a função corrente , integrando as componentes da velocidade ( e ).
A primeira etapa para fazer isso é usar a fórmula de cálculo de e em função de (equações 9-20 do livro) e substituir as equações de e dadas pelo enunciado.
Passo 3
Agora vamos integrar a equação de em relação a e encontrar a função corrente . Dizendo isso de outra forma, vamos pensar qual função que, ao ser derivada parcialmente em relação a , seria igual a .
Depois da integração em , encontramos que é a soma entre um termo em função de e uma função de . Ou seja, a função, cuja derivada parcial em vale é a soma entre um termo em função de e outro em função de . Mas por que tem uma função de nessa integração, se só houve integração em relação à variável ?
Isso ocorre, porque quando derivamos parcialmente a função em relação a , os termos que são funções de são considerados constantes! Ou seja, nada mais é do que a constante de integração da integral em !
Para achar , temos que derivar parcialmente em a função que encontramos.
Passo 4
Derivando parcialmente , achamos que:
onde é a derivada de .
Substituindo a fórmula de nessa equação:
Agora podemos integrar essa derivada em relação a para achar .
onde é uma constante de integração.
Substituindo isso na fórmula de , achamos:
Isso quer dizer que para encontrar , só precisamos achar .
Passo 5
Para achar o valor de , temos que lembrar que a função vale zero para igual a .
Substituindo essa nova informação na equação de , achamos:
Passo 6
Com a equação de nós somos capazes de achar o valor da vazão volumétrica por unidade de largura que passa entre as linhas de corrente e . Fazemos esse cálculo adaptando a equação 9-25 do livro para o nosso caso. Essa equação se encontra abaixo.
Essa equação mostra que, para encontrar precisamos do valor de .
é obtido substituindo na equação de .
Substituindo esse novo valor na equação de , achamos o valor de .