Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 44

Quando uma corrente uniforme escoa sobre um cilindro rombudo imerso, uma grande esteira de baixa velocidade é criada a jusante, idealizada com uma forma em V como mostra a figura abaixo. As pressões p 1 e p 2 são aproximadamente iguais. Se o escoamento é bidimensional e incompressível, com largura b normal ao papel, deduza a fórmula para a força de arrasto F sobre o cilindro. Reescreva seu resultado na forma de um coeficiente de arrasto adimensional baseado no comprimento do corpo, C D = F ρ U 2 b L

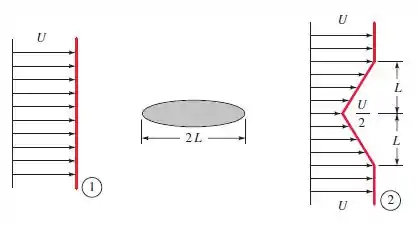
Passo 1

Vamos propor inicialmente um volume de controle como mostrado abaixo. Vamos escrever então a equação da continuidade para um estado estacionário.

0 = ∫ ρ u d A z - ∫ ρ u d A 1 = 2 ∫ 0 L ρ U 2 1 + y L b d y - 2 ρ U b H

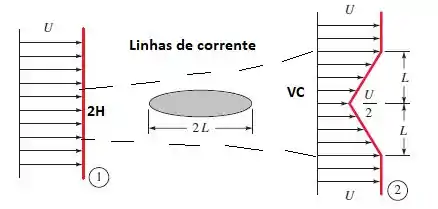
Onde 2H é a altura da entrada de fluido. Se resolvermos essa igualdade para H, vamos encontrar que H = 3 L 4

Passo 2

Agora, a relação de momento linear é utilizada. Note que a força de arrasto F é para a direita, então a força que responderá a ela deve estar direcionada para a esquerda.

∑ F x = 0 = ∫ z u ρ u   d A - ∫ 1 u ρ u   d A

∑ F x = 0 = 2 ∫ 0 L U 2 1 + y L ρ U 2 1 + y L b d y - 2 H ρ U 2 b = - F a r r a s t o

Lembrando que H = 3 L 4 , a força de arrasto deve ser:

F a r r a s t o = 3 2 ρ U 2 L b - 7 6 ρ U 2 L b = 1 3 ρ U 2 L b

Passo 3

Ou seja, nosso coeficiente de arrasto é dado por:

C D = F ρ U 2 L b = 1 3 ρ U 2 L b ρ U 2 L b = 1 / 3

Resposta

C D = 1 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

4.99 Um pequeno objeto redondo é testado em um túnel de vento de 0,75 m de diâmetro. A pressão é uniforme nas seções 1 e 2. A pressão a montante é 30 mm de H 2 O (manométrica), a pressão a jusante é 1
4.109 Quando um jato plano de líquido atinge uma placa inclinada, ele se parte em duas correntes de velocidades iguais, mas de espessuras desiguais. Para escoamento sem atrito, não pode haver força ta
4.106 Ar, na condição-padrão, escoa no longo de uma placa plana. A velocdiade da corrente livre, não perturbada, é U 0 = 20m / s . Em L = 0,4m a jusante da borda de ataque da placa, a espessura da cam
4.105 Um fluido com massa específica ρ = 750k g / m 3 escoa ao longo de uma placa plana de largura 1 m. A velocidade da corrente livre, não perturbada, é U 0 = 10m / s . Em L = 1m a jusante da borda d
4.104 Considere o escoamento incompressível de um fluido em uma camada-limite como descrito no Exemplo 4.2. Mostre que a força de arrasto devido ao atrito do fluido sobre a superfície é dada por F f =