Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 2.Exercício - Ex. 47

Um cubo de peso específico γ c flutua num líquido de peso específico γ l . Determinar a relação γ c / γ l para que o cubo flutue com as arestas na vertical.

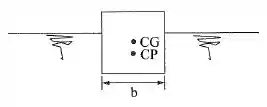
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Como o cubo flutua, o empuxo será igual ao peso do cubo. Temos que:

E = G

Desenvolvendo, temos que:

γ L V s u b = γ c V c

γ L A h s u b = γ c A h c

Logo:

h s u b = γ c γ L b

Para efeito de cálculo, vamos chamar x = γ c γ L , portanto:

h s u b = x b

Passo 2

Podemos definir a distância entre o centro de gravidade e o centro de pressão como:

l = b 2 - h s u b 2

Substituindo h s u b , temos que:

l = b 2 - x b 2

Pela teoria temos que r que é a altura metacêntrica, para um corpo que flutua, deve ser maior que zero, logo:

r > 0

Podemos definir r como:

γ I y G - l > 0

Substituindo os valores conhecidos, temos que:

γ l I y γ c V c - l > 0

I y x b 3 - l > 0

Logo:

b 4 12 x b 3 - b 2 - x b 2 > 0

Passo 3

Simplificando a expressão do passo anterior, temos que:

b 12 x - b 2 + x b 2 > 0

Multiplicando por 12 x e dividindo por b temos que:

1 - 6 x + 6 x 2 > 0

6 x 2 - 6 x + 1 > 0

Resolvendo a equação do segundo grau, temos que:

x 1 = 0,21

E:

x 2 = 0,79

O que nos leva a concluir que:

0 < x < 0,21

0 < γ c γ L < 0,21

E:

0 , 79 < x < 1

0 , 79 < γ c γ L < 1

Resposta

0 < γ c γ L < 0,21

0,79 < γ c γ L < 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere um cilindro de madeira ( d = 0,6 ) de 1m de diâmetro e 0,8m de comprimento. Esse cilindro seria estável se colocado para flutuar com seu eixo na vertical em óleo ( d = 0,8 ) ?
A idealização do iceberg do Problema P2.128 pode se tornar instável se seus lados derreterem e sua altura exceder sua largura. Na Figura P2.128 considere que a altura seja L e a profundidade normal ao
Considere que o balão do Problema P2.111 seja construído para ter um diâmetro de 14m , cheio ao nível do mar com ar quente a 70 ℃ ℃ e 1a t m , e seja liberado. Se o ar dentro do balão permanecer const
Uma barcaça tem 4,5m de largura e 12m de comprimento e flutua com um calado de 1,2m . Ela recebe uma carga de cascalho tal que seu centro de gravidade está 0,6m acima da linha d’água. Ela é estável?
Um bloco de madeira ( d =0,6 ) flutua em um fluido X , como na Figura P2.126, de forma que 75 % de seu volume está submerso nesse fluido. Calcule a pressão vacuométrica do ar no tanque.