Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 39

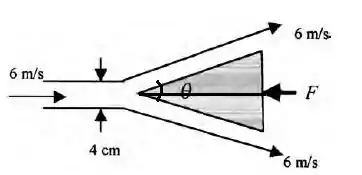
Uma cunha divide uma lâmina de água a 20°C, como mostra abaixo. Tanto a cunha quanto a lâmina de água são muito longas na direção normal ao papel. Se a força necessária para manter a cunha estacionária for de F = 124 N por metro de largura, qual é o ângulo θ   da cunha?

Passo 1

E aí, genteeeee! Tudo bem? Vamos encarar nosso “lerigou da mecflu”? Então lerigou!!! Hehe

Vamos primeiro de tudo assumir que o escoamento é uniforme, beleza?

E como estamos falando de força, precisamos de alguma forma lembrar de alguma equação que tenha força pra gente conseguir fazer nossos cálculos, certo? E qual é a melhor maneira? Vamos aplicar o balanço de momentooo!!!

Mas pera!! Eu só tô vendo uma força aplicada ali no desenho, onde está a outra? Aí vem o pulo do gato!!! Você concorda comigo que o escoamento tem uma força aplicada no sentindo contrário de F, certo? Mas como escrever isso??

Passo 2

Como começamos a discutir, precisamos verificar que força é essa que é contrária a F.

A gente primeiro vai lembrar que F = m * a = k g m s 2 = N

Hummmmmmmmmm, olha que maneiro!!!! Se você fizer m ˙ e u e = k g s m s = k g m s 2 = N

OPAAAAAAAAAAAAAAAAAA então o produto da vazão mássica pela velocidade de escoamento dá pra gente FORÇA EXERCIDADA do escoamento.

Então, pelo balanço de forças vamos ter que na direção X

∑ F x = m ˙ e u e x - F = 0

Vamos assumir que a largura normal ao papel terá comprimento unitário para facilitar nossos cálculos.

Passo 3

Agora fica bem mais tranquilo de fazermos as contas, se liga!!!

m ˙ e = ρ A V = 998 0,04 × 1 6 = 239,5   k g / s

- F = - m ˙ e u e x

Por trigonometria temos que u e x = u e cos ⁡ θ 2 .

F = 124 × 1  

F = 124   N

124 ×   1 = - 239,5   × 6 ×   cos ⁡ θ 2 - 1

124 = - 1437 cos ⁡ θ 2 - 1

cos ⁡ θ 2 = 1 - 124 1437

θ = 2 cos - 1 ⁡ 1 - 0.08629

θ = 47.954 °

θ ≅ 48 °

Resposta

θ = 48 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a mesma vazão no mesmo sistema rotativo do Problema 4.191 for não uniforme, mas variar linearmente de um máximo no raio externo até zero no raio interno, determine:a) O torque requerido para manter
4.88 Uma cabeça cônica de jateamento é mostrada. O fluido é a água e a corrente de saída é uniforme. Avalie (a) a espessura do jato em forma de cortina de água no raio de 400 mm e (b) a força axial ex
4.91 Uma bomba a jato de água tem área do jato de 0,009 m² e velocidade do jato de 30,5 m/s. O jato está dentro de uma corrente secundária de água com velocidade V = 3m / s . A área total do duto (a s
4.90 Uma montagem com um bocal curvo que descarrega para a atmosfera é mostrada. A massa do bocal é 4,5 kg e seu volume interno é de 0,002 m³. O fluido é a água. Determine a força de reação exercida p
4.92 Um cotovelo redutor de 30° é mostrado. O fluido é água. Avalie as componentes da força que deve ser aplicada pelos tubos adjacentes para manter o cotovelo estático.