Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 26

Uma fina camada de líquido escorrendo sobre um plano inclinado, como mostra a seguir, terá um perfil de velocidades laminar, u ≈ U o 2 y h - y 2 h 2 , em que U o é a velocidade na superfície. Se o plano tem largura b normal ao papel, determine a vazão volumétrica do filme. Suponha que h = 12,7 mm e que a vazão para cada metro de largura do canal seja dada por 15,52 L/min. Calcule U o em m/s.

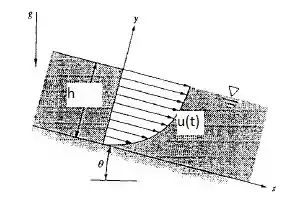
Passo 1

Fala ae, galera!! Vamos arrasar em mais um exercício de mecflu?

A gente que a vazão volumétrica é dada pelo produto entre a área e a velocidade média, lembrando que quando temos um perfil de velocidade precisamos integrar o perfil em relação a área transversal de escoamento.

Vamos dar uma olhada em como o fluido está enxergando a área transversal?

Q = ∫ u d A = ∫ 0 x = z ∫ 0 y = h U 0 2 y h - y 2 h 2 d y d x

Q = U 0 z ∫ 0 y = h 2 y h - y 2 h 2 d y = U 0 z 2 y 2 2 h - y 3 3 h 2 0 h = U 0 z 2 h 2 2 h - h 3 3 h 2 = U 0 z h - h 3

Q = 2 3 U 0 z h

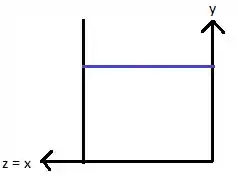
Passo 2

Supondo h = 12,7 mm e Q = 15,52 L/min para cada metro de largura, vamos antes de mais nada converter essas unidades aí pra SI, beleza?

h = 12,7   m m = 12,7   x 10 - 3 m

Q = 15,52 L m i n x m i n 60 s x m 3 1000 L = 2,58   x   10 - 4   m 3 / s

Passo 3

Agora que conhecemos a vazão, precisamos encontrar a velocidade. Para isso, basta escrevermos a vazão em função da velocidade e área transversal de escoamento.

Q = U A = U z h → U = Q z h = 2,58   x   10 - 4 1   x   12,7   x   10 - 3 = 0,2   m / s

Resposta

U = 0,2   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um líquido viscoso é drenado de um tanque circular, com diâmetro D = 300m m , através de um longo tubo circular de raio R = 50m m . O perfil de velocidade no tubo de descarga é u = u m i x 1 - r R 2 M
Água escoa em regime permanente sobre uma placa plana porosa. Uma sucção constante é aplicada ao longo da seção porosa. O perfil de velocidade na seção c d é u U ∞ = 3 y δ - 2 y δ 3 / 2 Avalie a vazão
Um funil cônico, com meio ângulo θ = 15 ° , com diâmetro máximo D = 70m m e altura H , deixa escapar líquido por um orifício (diâmetro d = 3,12m m ) no seu vértice. A velocidade do líquido deixando o
Um tanque cilíndrico de diâmetro D = 50m m , possui o esgoto por uma abertura de diâmetro d = 5m m , em seu fundo. A velocidade do líquido saindo do tanque é aproximadamente V = 2 g h , em que y é a a
Para as condições do Problema 4.48, estime o tempo requerido para drenar o tanque à profundidade de y = 0,3m (uma mudança na profundidade de 0,1m ), e de y = 0,3m para y = 0,2m (também uma mudança na