Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 10.Problemas - Ex. 96
Dados medidos do desempenho das turbinas de reação da represa e Shasta Dam, perto de Reddin, na Califórnia, são mostrados na Fig. 10.39. Cada turbina tem potência nominal de 77.10³ kW, quando operada a 138,6 rpm, sob uma altura de carga líquida de 115 m. Avalie a velocidade específica e calcule o torque no eixo desenvolvido por cada turbina nas condições nominais de operação. Calcule e trace a vazão de água, por turbina, necessária para produzir a potência nominal como uma função da altura de carga.
Passo 1
Tá legal! Vamos começar esse calculando a velocidade específica nas condições nominais de operação, então:
Substituindo os valores conhecidos (atentando para as unidades que devem ser utilizadas, rpm, kW e m), temos:
Passo 2
Para estimar o torque no eixo desenvolvido por cada turbina nas condições de operação, podemos usar a seguinte relação para a potência:
Substituindo os valores conhecidos, temos:
Passo 3
Agora, para estimar a vazão máxima através de cada turbina, vamos escrever a equação para a potência útil da turbina:
Isolando a vazão e deixando em função da altura de carga como pede-se no enunciado, temos:
Agora precisamos olhar para o gráfico da figura 10.39:
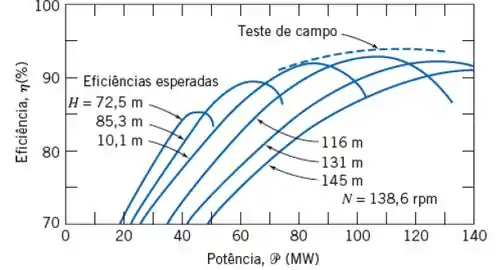
Observe que no nosso exercício temos a mesma rotação utitiliza nos ensaios para plotar o gráfico acima. Então para uma carga líquida de 115 m e potência de 77 MW, temos uma eficiência correspondente de:
Então, substituindo os valores conhecidos na equação para a vazão, temos:
Passo 4
Agora, para plotar a curva pedida no enunciado, precisamos de mais alguns pontos, então, para uma carga líquida de 101 m, com o auxílio do gráfico, temos:
E a vazão será:
Agora, para uma carga líquida de 131 m, temos uma eficiência de:
E a vazão será:
E, para uma carga líquida de 145 m, a eficiência será:
E a vazão será:
Então, plotando todos esses resultados em um gráfico, temos:
