Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 10.Problemas - Ex. 106
Um avião a jato viajando a 225 m/s aspira 50 kg/s. Se a eficiência propulsiva (definida como a razão do trabalho útil de saída e a energia mecânica de entrada para o fluido) do avião é 45%, determine a velocidade de descarga em relação ao avião.
Passo 1
Tá legal! Vamos começar o exercício ilustrando o problema e definindo o sistema de controle:
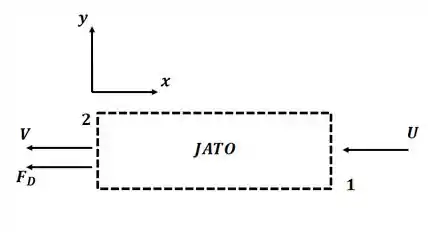
Então, vamos começar aplicando a equação para o equilíbrio de momento na direção vista no capítulo 4, então, temos:
Nesse caso, podemos desprezar as forças de campo atuando na direção , então temos , como temos regime permanente, podemos desprezar também a primeira integral com a derivada no tempo, então a equação se torna:
Agora, da continuidade do sistema, sabemos que:
E sabemos também da figura que e , então, substituindo os valores conhecidos na equação de cima, temos a força gerada pelos motores do jato:
Passo 2
Agora precisamos analisar a equação de energia, que também foi vista no capítulo 4, para o sistema, então, temos:
Como não temos calor entrando ou saindo do sistema, temos , não temos força de cisalhamento ou trabalhos sobre o sistema que não a potência do jato, então . Como o regime de escoamento é permanente, podemos desprezar também a integral com a derivada parcial no tempo e a equação se resume a:
A única propriedade do escoamento que varia nesse caso é a velocidade entre os pontos 1 e 2, então podemos cancelar todos os outros pontos. Vimos no passo 2 a continuidade do sistema, que nos dava:
E, também sabemos, do esquema do passo 1, que e que , então, a equação anterior se torna:
Esse trabalho é o trabalho ideal do sistema, sem considerar perdas.
Passo 3
Então para encontrar a velocidade de descarga, precisamos primeiro encontrar o trabalho útil gerado pelo sistema, que pode ser encontrado multiplicando a força encontrada no passo 1 pela velocidade de viagem do jato, então, temos:
Substituindo a expressão encontrada para no passo 1, temos:
E, então, a eficiência pode ser escrita como:
Substituindo as expressões encontradas e o valor da eficiência dado no enunciado, temos:
Substituindo os valores conhecidos, temos: