Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 10.Problemas - Ex. 93
As condições na entrada do bocal de uma turbina Pelton são e . O diâmetro do jato é e o coeficiente de perda do bocal é . O diâmetro da roda é . Para esta condição de operação, . Calcule (a) a potência produzida, (b) a velocidade normal de operação, (c) a velocidade aproximada de descarga, (d) o torque na velocidade normal de operação e (e) o torque aproximado para velocidade nula.
Passo 1
Tá legal! Vamos começar esse exercício aplicando a equação 10.28b para o sistema entre os pontos dentro da tubulação (1) e na saída do jato (2), então, temos:
Nesse caso, podemos desprezar as diferenças entre as cotas e , e como temos que o bocal descarrega para a atmosfera , e dessa forma, iremos utilizar a pressão dada de forma manométrica. Sabemos também que foi dado no enunciado e que , então a equação se torna:
E, como só temos perda localizada no bocal então:
Substituindo esse valor na expressão anterior, temos:
Substituindo os valores conhecidos:
Essa é a velocidade de descarga pedida na letra c).
Passo 2
Agora vamos calcular a vazão do sistema:
E, agora vamos encontrar a carga líquida para o sistema, dada por:
E, com isso, podemos encontrar a potência produzida pedida na letra a):
Substituindo os valores conhecidos:
Passo 3
Agora vamos encontrar a velocidade normal de operação, que será encontrada através da figura 10.36 junto com a eficiência de 0,86 dada no enunciado, então, temos:
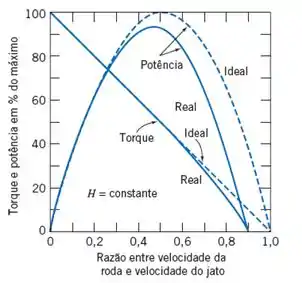
Então, para a eficiência de 0,86, temos uma razão de:
E, com isso podemos encontrar a velocidade angular de operação:
Passo 4
Como vimos a velocidade de descarga é igual a velocidade do jato, então, a velocidade angular de descarga será:
Passo 5
Então, conforme vimos nessa seção, sabemos que o torque ideal para uma turbina Pelton pode ser dado por:
Então, substituindo os valores conhecidos, temos:
Dessa forma, o torque na velocidade normal de operação pode ser encontrado utilizando a eficiência do sistema, então, temos:
Passo 6
Agora, para encontrar o torque aproximado para velocidade nula, devemos usar a fórmula do torque ideal, só que agora com , então, temos:
Então, substituindo os valores conhecidos, temos:
Esse já é o torque aproximado para a velocidade nula, pois como o sistema está em repouso, não precisamos multiplicar esse valor pela eficiência do sistema.