Deduza uma expressão para a ascensão capilar de um líquidos entre duas placas paralelas grandes, distantes entre si. , mergulhadas verticalmente no líquido. Considere que o ângulo de contato seja .

A melhor forma de começar é desenhando um esqueminha pra poder visualizar melhor o que o enunciado disse!

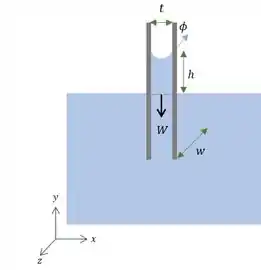
Temos então as nossas duas placas paralelas grandes mergulhadas verticalmente no líquido e queremos achar uma expressão na ascenção capilar. Em outras palavras a gente quer uma expressão de ! Beleza?

Na nossa figura temos que é a altura do capilar e e são a distancia entre as placas e o comprimento da placa, respectivamente. Eles consequentemente vão ser a espessura e o comprimento do capilar! E por fim, mas não menos importante, temos que é o ângulo de contato dado no enunciado.

O enunciado não da essa icógnita, , pra a gente, mas jájá vamos ver que ela é bastante necessária!

O valor da ascensão capilar entre as placas é determinado pelo equilíbrio de forças da coluna líquida retangular de altura . É importante a gente falar aqui que a pressão nesse ponto tracejado é igual a pressão na superfície livre do líquido, ambas são iguais a , isso equilibra a pressão atmosférica que atua sobre a superfície do capilar, desse modo esses dois efeitos cancelam-se mutuamente. O peso da coluna líquida pode ser calculado como:

Onde é a densidade do líquido, é aceleração da gravidade e é o seu volume, dado por:

Igualando o componente vertical da força de tensão superficial ao peso, temos:

Onde é dado por:

Onde é a tensão superficial do líquido, é o perímetro de contato do líquido com a placa e é o ângulo de contato dado no enunciado. é dado por:

Considerando o comprimento da placa e multiplicado por dois, por ser duas placas.

Substituindo, temos:

Isolando :

Agora podemos calcular a altura do capilar!!