Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 94

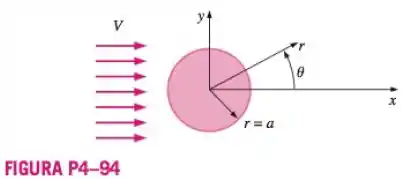
Existem várias ocasiões em que um escoamento de corrente livre razoavelmente uniforme encontra um cilindro longo normal ao escoamento (Figura P4-94). Os exemplos incluem o ar ecoando ao redor de uma antena de automóvel, o vento soprando contra um mastro de bandeira ou poste de telefone, o vento atingindo fios elétricos e as correntes oceânicas atingindo as vigas redondas e submersa que suportam as plataformas de petróleo. Em todos esses casos o escoamento na parte traseira do cilindro é separado em regime permanente e em geral turbulento. Entretanto, o escoamento na metade dianteira do cilindro é muito mais estacionário e previsível. Na verdade exceto por uma camada limite muito fina próxima á superfície do cilindro, o campo de escoamento pode ser aproximado pelas seguintes componentes de velocidade permanentes e bidimensionais do plano x y ou r θ :

u r = V cos ⁡ θ 1 - a 2 r 2               u θ = - V   s e n   θ 1 + a 2 r 2

Esse campo de escoamento é rotacional ou irrotacional? Explique.

Passo 1

Dado o campo da velocidade temos que determinar se o fluxo é rotacional ou irrotacional.

Assumindo que o fluxo é constante e que ele opera em duas dimensões r - θ .

Como temos as componentes da velocidade em um cilindro circular de raio r .

u r = V cos ⁡ θ 1 - a 2 r 2               u θ = - V   s e n   θ 1 + a 2 r 2             1

Desde que assumimos que o fluxo opera em duas dimensões em r - θ . A única componente zero do escoamento é na direção z . Em coordenadas cilíndricas temos:

ζ z = 1 r ∙ ∂ r u θ ∂ r - ∂ u r ∂ θ                 2

Passo 2

Para determinarmos se o fluxo é rotacional ou irrotacional temos que determinar sua componente z substituindo a equação (1) na equação (2), temos:

ζ z = 1 r ∙ ∂ r ∙ - V   s e n   θ 1 + a 2 r 2 ∂ r - ∂ V cos ⁡ θ 1 - a 2 r 2 ∂ θ

Aplicando as derivadas:

ζ z = 1 r ∙ - V   s e n   θ + V a 2 r 2 s e n   θ + V   s e n   θ - V a 2 r 2 s e n   θ

Como temos termos iguais de sinais diferentes temos:

ζ z = 1 r ∙ 0

ζ z = 0

Consequentemente, desde que o escoamento é totalmente zero, o fluxo é irrotacional.

Resposta

Consequentemente, desde que o escoamento é totalmente zero, o fluxo é irrotacional.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o escoamento de Couette — o escoamento entre duas placas paralelas infinitas separadas pela distância h , com a placa superior se movendo e a placa inferior fixa, como ilustra a Figura P 7 -
Considere a forma geral do teorema de transporte de Reynolds (TTR) dada por d B s i s t d t = d d t ∫ ρ b d V + ∫ ρ bV r → ∙ n → d A onde V r → é a velocidade do fluido com relação à superfície de con
Combine seus resultados do Problema 4 - 72 para formar o tensor de taxa de deformação bidimensional ε i j . ε i j = ε x x ε x y ε y x ε y y Os eixos x e y são principais?
Para o escoamento de Couette da Figura P 4 - 71 , calcule as taxas de deformação linear nas direções x e y , e calcule a taxa de deformação por cisalhamento ε x y .
Compare os resultados do Problema 4 - 79 e 4 - 84 e comente sobre a taxa de deformação linear na direção x .