Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 90

Aproximamos o escoamento do ar em um acessório de aspirador de pó seguindo as componentes da velocidade no plano central (o plano x y ):

u = - V ˙ x π L x 2 + y 2 + b 2 x 4 + 2 x 2 y 2 + 2 x 2 b 2 + y 4 - 2 y 2 b 2 + b 4

E

v = - V ˙ y π L x 2 + y 2 - b 2 x 4 + 2 x 2 y 2 + 2 x 2 b 2 + y 4 - 2 y 2 b 2 + b 4  

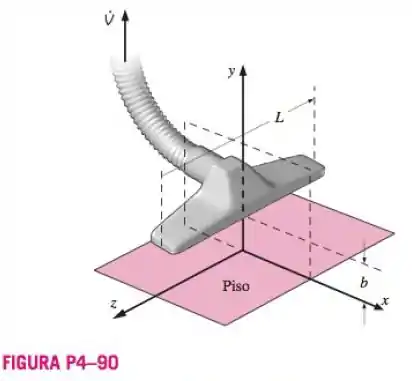
Onde b é a distância do acessório acima do piso, L é o comprimento do acessírio e V ˙ é a vazão em volume do ar sendo sugado para dentro da mangueira(FiguraP4-90). Determine o local dos pontos de estagnação nesse campo de escoamento.

Passo 1

Temos que determinar a posição do ponto de estagnação no campo de velocidade dado.

Temos que assumir que o fluxo é constante e que o fluxo ocorre em duas dimensões no plano x - y .

Note que nós temos a equações de velocidade de cada componente x e y , e sabemos que para o ponto de estaquinação temos que u e v tem que ser igual a zero. Portanto, nosso objetivo é analisar em quais situações isto pode ser possível.

Passo 2

Temos que as equações das componentes de velocidade são:

u = - V ˙ x π L x 2 + y 2 + b 2 x 4 + 2 x 2 y 2 + 2 x 2 b 2 + y 4 - 2 y 2 b 2 + b 4         ( 1 )

E

v = - V ˙ y π L x 2 + y 2 - b 2 x 4 + 2 x 2 y 2 + 2 x 2 b 2 + y 4 - 2 y 2 b 2 + b 4         ( 2 )

Nomeando equação da velocidade da componente x como equação 1 e da componentes y como 2 .

Agora vamos analisar as equações,

note que para equação 1 , para u = 0 é possível se x = 0 ou x 2 + y 2 + b 2 = 0 .

Para equação 2 , para v = 0 é possível se y = 0 ou se x 2 + y 2 - b 2 = 0 .

Com estes pontos levantados, temos que o ponto de estagnação , para u = 0   e   v = 0 , será a origem x , y = 0,0 .

Resposta

Com estes pontos levantados, temos que o ponto de estagnação, para u = 0   e   v = 0 , será a origem x , y = 0,0 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o escoamento de Poiseuille totalmente desenvolvido e bidimensional – o escoamento entre duas placas paralelas finitas separadas pela distância h , com as placas superior e inferior fixas, e
Considere a forma geral do teorema de transporte de Reynolds (TTR) dada no Problema 4-75. Seja B s i s o momento m V → de um sistema de partículas de fluido. Sabemos que para um sistema, a segunda lei
Repita o problema 4 - 83 , exceto que a tinta é introduzida de t = 0 a t = 10 s e as linhas de emissão devem ser traçadas em t = 12s em vez de 10s .
Para o escoamento de Poiseuille bidimensional do Problema 4-79, calcule as taxas de deformação linear nas direções x e y e calcule a taxa de deformação por cisalhamento ε x y .
Considere a forma geral do teorema de transporte de Reynolds (TTR) dada no Problema 4-75. Seja B s i s o momento angular H → =r →× mV → de um sistema de partículas de fluido, onde r → é o braço do mom