Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 96

Considerando a metade a montante x < 0 doo campo de escoamento do Problema 4-94 (escoamento sobre um cilindro circular) . Introduzindo um parâmetro chamado função de corrente ψ , que é constante ao longo das linhas de corrente dos escoamentos bidimensionais como aquela considerada aqui (Figura P4-96). O campo de velocidade do Problema 4-94 corresponde a uma função de corrente dada por

ψ = V   s e n   θ r - a 2 r

(a) Tomando ψ constante, gere uma equação para uma linha de corrente. (Sugestão: Use a fórmula quadrática para solucionar r como função de θ .).

(b) Para o caso particular em que v = 1,00   m / s e o raio do cilindro a = 10,0   c m , trace várias linhas de corrente na metade a montante de escoamento 90 ° < θ < 270 ° . Por questões de consistência, trace-as no intervalo - 0,4   m < x < 0   m ,   - 0,2   m < y < 0,2   m , com valores da função de corrente espaçados uniformemente entre - 0,16   m 2 / s e 0,16   m 2 / s .

Passo 1

Temos a função de corrente e temos que encontrar a equação que regem para as linhas de fluxo, e por final utilizar o caso particular e plotar estas linhas.

Assumindo que o fluxo é constante e que ele opera apenas em duas dimensões plano r - θ .

Passo 2

a)Bem como dito anteriormente temos a função de corrente

ψ = V   s e n   θ r - a 2 r

E seguiremos a dica que nós foi dada que executar por meio da fórmula quadrática, cara em outras palavras ele esta pedindo pra resolver por Bhaskara.

Primeiro iremos multiplicar os dois lados da equação por r e resolveremos a equação de Bhaskara para r .

r ∙ ψ = V   s e n   θ r - a 2 r ∙ r

Rearranjando a equação:

r 2 V   s e n   θ - r   ψ - a 2 V   s e n   θ = 0

Agora ficou tranquilo de identificar nossos termos, aplica a formula de Bhaskara, temos:

r = ψ ± ψ 2 + 4 a 2 V 2 s e n 2 θ 2 V   s e n   θ

E está é nossa equação que regem a linhas de fluxo.

Passo 3

b) Para o caso particular em que V = 1,0   m / s e o raio do cilindro é a = 10,0   c m , nós escolhemos vários valores de ψ e utilizando a formula que foi desenvolvida no item (a), podes fazer a seguinte imagem, que cara único valor de ψ corresponde unicamente a uma linha de fluxo.

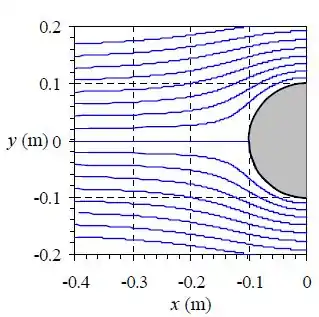
As linhas de fluxo que correspondem um fluxo passando a um cilindro circular.

Resposta

a) r = ψ ± ψ 2 + 4 a 2 V 2 s e n 2 θ 2 V   s e n   θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Combine seus resultados do Problema 4 - 88 para formar o tensor taxa de deformação simétrico ϵ y . ϵ i j = ϵ r r ϵ r x ϵ x r ϵ x x Os eixos x e r são principais?
Considere o escoamento de Poiseuille bidimensional do problema 4-79. O fluido entre as placas é água a 40 ° C . Seja h = 1,6 m m a altura da lacuna e d P d x = - 230 N / m 3 o gradiente de pressão. Ca
Considere o escoamento de Poiseuille bidimensional do problema 4 - 79 . O fluido entre as placas é água a 40° C . Seja h = 1,6m m a altura da lacuna e d P / d x = - 230N / m 3 o gradiente de pressão.
O escoamento de duto convergente é modelado pelo campo de velocidade em regime permanente e bidimensional do Problema 4-15. Use a taxa de deformação volumétrica para verificar se esse campo de escoame
Usando os resultados do Problema 4-58: ( a ) Esse escoamento é rotacional ou irrotacional? ( b ) Calcule a componente z da vorticidade para esse campo de escoamento.