Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 117

A densidade de um corpo flutuante pode ser determinada ligando-se pesos ao corpo até que o corpo e os pesos estejam completamente submersos e, em seguida, pesando-os separadamente no ar. Considere uma tora de madeira que pese 1.154   N no ar. Se forem precisos 34   k g de chumbo ( ρ = 11.300   k g / m 3 ) para afundar completamente a tora e o chumbo na água, determine a densidade média da tora.

Passo 1

Temos que determinar a densidade média da tora por está medida indireta.

Temos as seguintes propriedades à densidade do nosso pesinho é ρ p e s o = 11300   k g / m 3 e a densidade da água tomaremos como padrão ρ w = 1000   k g / m 3 .

Devemos ficar a tentos a formula original de densidade,

ρ = m V

Pois, este exercício pode ser resolvido apenas com está lógica e de que estamos trabalhando apenas com um corpo só.

Passo 2

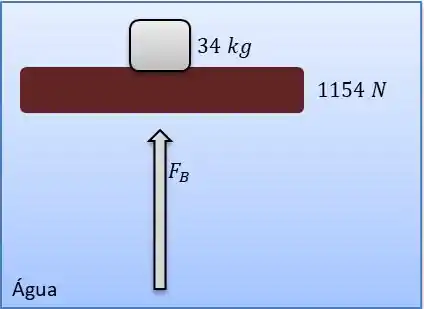
Analisando que o nossa madeira deve possui uma peso igual à força flutuante F B , pois a madeira inicialmente se encontra flutuando no fluido e o peso faz com que ela seja totalmente submersa, com isto temos que a força vertical está balanceada devido ao equilíbrio estático. Neste caso temos a densidade média do corpo deve ser igual à densidade do fluido desde que

P e s o = F B

ρ m a d e i r a g V = ρ w g V

ρ m a d = ρ w

Portanto, temos que a densidade média pode ser dada por:

ρ m é d i o = m t o t a l V t o t a l = m p e s o + m m a d e i r a V c h u m b o + V m a d e i r a = ρ w

Desta equação podes determinar o volume da madeira, e com as informações do enunciado podemos calcular o volume do chumbo e a massa da madeira, vamos lá?

Do enunciado o volume do chumbo, fica:

V c h u m b o = m c h u m b o ρ c h u m b o = 34 11300 = 3,01 ∙ 10 - 3 m 3

E massa da madeira pode ser calculada pelo seu peso:

m m a d e i r a = P e s o g = 1540 9,81 = 157   k g

Passo 3

Retomando a equação que escrevemos anteriormente:

ρ m é d i o = m t o t a l V t o t a l = m p e s o + m m a d e i r a V c h u m b o + V m a d e i r a = ρ w

Como calculamos o volume do chumbo, a massa da madeira e temos a densidade da água, podemos agora calcular o volume da madeira:

m p e s o + m m a d e i r a V c h u m b o + V m a d e i r a = ρ w

Isolando o volume da madeira:

V m a d e i r a = V c h u m b o + m p e s o + m m a d e i r a ρ w

V m a d e i r a = 3,01 ∙ 10 - 3 + 34 + 157 1000 = 0,194   m 3

Agora que temos o volume da madeira podes determinar sua densidade:

ρ m a d e i r a = m m a d e i r a V m a d e i r a = 157 0,194 = 809   k g / m 3

Resposta

ρ m a d e i r a = 809   k g / m 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O tanque na figura abaixo tem largura de 2 m. Desprezando a pressão atmosférica, encontre a força hidrostática resultante no painel BC (a) com uma única formula e (b) calculando as forças horizontais
Considere a placa inclinada AB com comprimento L na figura abaixo. (a) A força hidrostática sobre a placa é igual ao peso da água que está faltando acima da placa? Se não for, corrija essa hipótese. D
Em 1960, o batiscafo Trieste de Auguste e Jacques Picard bateu um recorde descendo a uma profundidade de 10912 m no Oceano Pacífico, próximo de Guam. A esfera que alojava o passageiro tinha 2,1 m de d
A comporta AB tem comprimento L e largura b, está articulada em B e tem peso desprezível. O nível h do líquido permanece no topo da comporta para qualquer ângulo θ . Encontre uma expressão analítica p
A comporta B da figura abaixo tem 30 cm de altura, 60 cm de largura e é articulada no seu topo. Qual a profundidade h de água na qual terá início a abertura da comporta?