Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 116
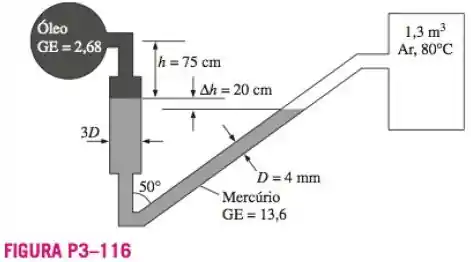
Uma tubulação de óleo e um tanque rígido de ar de estão conectados entre si por um manômetro, como mostra a Figura Se o tanque tiver de ar a , determine (a) a pressão absoluta na tubulação e (b) a variação de quando a temperatura do tanque cair até . Considere que a pressão na tubulação de óleo permaneça constate e que o volume de ar no manômetro seja desprezível com a relação ao volume de o tanque.
Passo 1
Temos que determinara pressão no tubo e variação de nível do fluido manométrico quando a temperatura do ar cai.
Assumindo que todos os líquidos são incompressíveis, o efeito da coluna de ar é insignificante e o volume do tanque de ar é insignificante comparado ao volume do tanque do manômetro.
Temos as seguintes propriedades, temos a gravidade específica do mercúrio como e 2,68 para o óleo, adotaremos a densidade padrão da água como e a constante do gás ideal do ar é .
Para letra (a) sabemos que a pressão no tanque do óleo é igual à pressão no tanque do ar, portanto tendo estes itens explanados, temos que para resolver está questão iremos começar com a pressão no tanque do óleo, e iremos movendo ao longo dos tubos (somando as pressões assim como vamos “andado” para baixo), diminuindo a pressão (assim como vamos para cima nos tubos) até chegar a no tanque do ar.
Passo 2
a) Executando oque foi dito no passo 1, temos:
Como desejamos pressão absoluta no tubo e o tubo esta repleto de óleo, portanto isolando :
Note que não possuímos a pressão do tanque do ar, mas podemos calcular com a formula do gás ideal:
Retomando o calculo inicial:
Substituindo as variáveis e coloca os termos em comum em evidencia:
Passo 3
b) Bem neste item temos duas coisas bem relevantes uma delas é a pressão no tanque do ar que ira diminuir devido à temperatura de cair também, então vamos já calcular isto:
E o outro item é que devido à variação de nível do mercúrio, após a variação da temperatura isto fará com que o mercúrio no braço esquerdo diminuirá em nível quanto que no braço direito ele aumentará em . Perceba que isso tudo ocorre e os volumes dos dois braços permanecem constantes, portanto podemos igualar o volume do braço esquerdo com a variação de “altura” igual o volume do braço direito com a variação de “altura” .
Isolando , pois com ele podemos calcular o nível de mercúrio e o acréscimo no nível de óleo, temos:
Mas note que referente a nível inclinado de mercúrio e desejamos o nível vertical, que chamaremos de . Portanto, perceba que temos um triangulo retângulo com um ângulo de , aplicando trigonometria neste triangulo temos que:
E finalmente saberemos que o nível de mercúrio aumentara em uma grandeza de:
Passo 4
Agora que possuímos a variação do nível de mercúrio (generalizada), podemos calcular agora em termos realmente em números quanto este mercúrio vaiou.
Retomando a equação de pressão, com a pressão do ar a uma temperatura de e com a variação calculada, fica:
Substituindo os valores e rearranjando a equação:
Resolvendo os cálculos e isolando :
Isso significa que após o decaimento da temperatura do tanque de ar, a interface óleo e mercúrio irá descer e a interface mercúrio e ar ira aumentar .
Resposta
a)
b)