Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 39
Para descongelar o gelo acumulado na superfície externa de um para-brisa de automóvel, ar quente é soprado sobre a superfície interna do para-brisa. Considere um para-brisa de automóvel com espessura de 5 mm e condutividade térmica de . A temperatura externa do ambiente é de e o coeficiente de transferência de calor por convecção é de , enquanto a temperatura ambiente no interior do automóvel é de . Determine o valor do coeficiente de transferência de calor por convecção para o ar quente soprando sobre a superfície interna do para-brisa necessária para fazer com que o gelo acumulado comece a derreter.
Passo 1
Muito bem galera !! O que queremos aqui?
Descobrir a coeficiente de transferência de calor por convecção do ar quente, , que será capaz de descongelar o para-brisa, certo?
Antes de qualquer coisa vamos assumir que a taxa de transferência de calor é constante e, portanto, a transferência de calor entre o ambiente externo e o para brisa é igual à transferência de calor entre o ar quente e o para-brisa:
Nós podemos calcular o calor externo como:
Sabendo que:
E considerando a área de superfície unitária:
Então:
Como a variação em graus Celsius e em kelvin é a mesma:
Passo 2
Beleza galera, agora que já sabemos a transferência de calor externa podemos assumir que:
Se lembram como calcular a transferência de calor através de uma superfície?
Para determinar a resistência total nós vamos desenhar, ok?
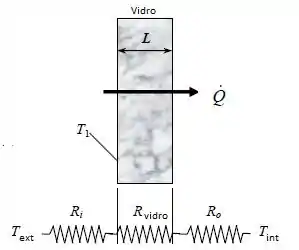
Como estamos considerando a troca de calor entre o vidro e o interior:
Já sabemos como calcula cada uma delas, não é?
Substituindo nossos dados:
Lançando na fórmula do calor:
Como a variação em graus Celsius e Kelvin são iguais:
Isolando o coeficiente:
Bem gostosa essa, não é ?!