Determinados a reduzir o custo semanal de associado à perda de calor através da porta de vidro por convecção e radiação, os inquilinos do Problema 9.18 cobriram a parte interna da porta com uma folha de isolante extrudado com de espessura. Como eles não são cuidadosos em relação à casa, o isolante não foi bem colocado, resultando em um espaço mm entre o isolante extrudado e a lâmina de vidro, que permite ao ar se infiltrar no espaço entre o vidro e o isolante.
Determine a perda de calor pela porta de vidro e o custo semanal associado ao isolante mal instalado em posição. O isolante reduzirá significativamente as perdas por radiação através da porta de vidro. As perdas serão quase inteiramente devido à convecção.
Represente graficamente as perdas térmicas pela porta de vidro como uma função do espaçamento entre o vidro e o isolante para .
Passo 1
Como primeiro passo, temos que buscar os dados do problema 9.18 e trazer para a física do problema atual, aqui eu trouxe um esboço da nova situação:
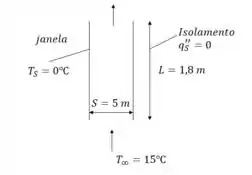
Agora, como seguimos normalmente determinando a temperatura média internamente para buscamos os parâmetros do fluido na tabela A-4 (Incropera - Fundamentos de Transferência de Calor e Massa - 7°Ed.):
Passo 2
Bom temos que na questão , é pedido a gente determine a perda de calor pela porta de vidro e o custo semanal associado ao isolante mal instalado em posição.
Além disso, a questão diz que basicamente, a física do problema se trata de convecção, desprezando as perdas por radiação devido ao isolante.
Portanto, temos que ter em mente, que o problema se trata de convecção natural em canais (Placas paralelas) e para condições isotérmicas, a correlação correspondente é:
Onde,
Passo 3
Muito bem, tendo as equações e mãos, basta calcularmos agora...
Passo 4
Muito bem, agora podemos determinar a perda de calor pela porta de vidro...
Portanto...
E o custo será...
Resposta
A perda de calor pela porta de vidro e o custo semanal associado ao isolante mal instalado em posição: