Um líquido de viscosidade escoa entre duas placas paralelas infinitas distantes 5 mm, com escoamento laminar. O gradiente de pressões ao longo do escoamento é . Determinar a tensão de cisalhamento na placa superior e a vazão em olume por unidade de profundidade.
Passo 1
Para resolver essa questão precisamos fazer as seguintes considerações:
- Escoamento unidirecional ao longo de
- Regime permanente
- A velocidade só varia o longo de
Se quiser saber os detalhes, abaixo eu explico direitinho cada uma das considerações:
A questão não especifica a orientação das placas, então vamos considerar que as placas são paralelas ao eixo , pois isso vai garantir que o escoamento é unidimensional:
E também vamos assumir que o regime é permanente:
Agora vamos olhar pro nosso escoamento. Como ele é viscoso, ele tem uma distribuição parabólica como mostrada na figura:
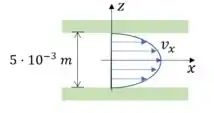
Isso demonstra que a velocidade varia ao longo de . A questão afirma que as placas são infinitas, isso nos permite assumir que o escoamento é completamente desenvolvido e por isso não varia ao longo de . Em outras palavras, é função apenas de :
E por fim, como estamos desconsiderando o eixo e a variação de energia potencial gravitacional ao longo de é muito pequena, podemos assumir que a pressão varia apenas no eixo
Passo 2
Com todas as considerações que fizemos a equação de Navier-Stokes se torna:
Mas perceba o seguinte, como a pressão só é função de ; e é função apenas de podemos tornar as derivadas parciais em derivadas totais.
Agora observe o macete da questão: como a pressão só é função de ; e é função apenas de , a igualdade acima só será verdadeira se o resultado das derivações for uma constante.
Então podemos separar as duas equações:
Passo 3
Mas e agora? Como vamos descobrir o valor de
Fácil, a questão diz que: O gradiente de pressões ao longo do escoamento é , em termos matemáticos:
O motivo do sinal negativo é porque sabemos que esse gradiente corresponde a uma queda de pressão.
Como só varia ao longo de :
Logo, o valor de é:
Passo 4
Agora temos:
Logo:
Integrando duas vezes termos:
Observando de novo o desenho:
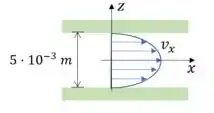
Percebemos que quando , aplicando:
E que quando , aplicando:
A equação final é:
Passo 5
A tensão de cisalhamento é definida por:
No ponto
Passo 6
Pela equação da continuidade, a velocidade média é dada por:
Vamos chamar a largura da placa de então a área de vazão é dada por:

Na integral
A integração ocorrerá entre e :