Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 13.Problemas - Ex. 17
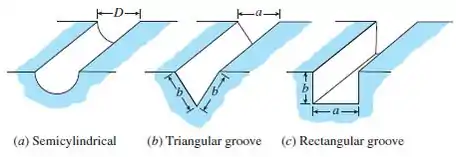
Determine o fator de forma das ranhuras muito longas mostradas na Fig. P13–17 para o lado externo, sem usar tabelas ou gráficos de fatores de forma. Despreze os efeitos das extremidades.
Passo 1
Vamos continuando, animados ??
Então bora lá !!
Na letra (a) nós podemos começar desenhando:
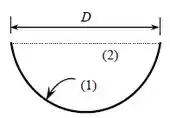
usando o somatório dos fatores de forma:
Como a radiação deixando uma superfície não a atinge:
Usando o somatório nós podemos calcular o outro fator de forma:
Como nós queremos o fator de forma da ranhura para o lado externo nós na verdade queremos o fator .
E como faremos?
Simples!! Basta usarmos a regra da reciprocidade:
Calculando as áreas:
E substituindo:
Vamos para a letra (b) ??
Passo 2
Agora nós vamos começar desenhando:
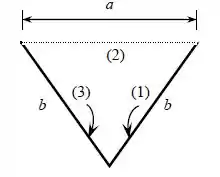
O que nós queremos aqui é vamos ter que usar alguns artifícios para acha-lo, certo?
Por ser superfícies simétricas:
Como a radiação deixando uma superfície não a atinge:
Então:
Pela reciprocidade:
Isolando o que queremos:
As áreas:
Substituindo:
Passo 3
Para a letra (c) nós temos a seguinte situação:
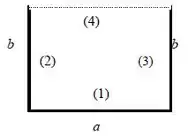
Novamente, por ser superfícies simétricas:
Como a radiação deixando uma superfície não a atinge:
Então:
Pela reciprocidade:
Isolando o que queremos:
As áreas:
Substituindo:
Tranquilinha?!