Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 54
13.54 Oxigênio líquido é armazenado em um vaso esférico com parede delgada e 0,8 m de diâmetro, que encontra-se no interior de um segundo vaso esférico, também com parede delgada e com 1,2 m de diâmetro. As superfícies dos vasos são cinzas, difusas e opacas, com uma emissividade de 0,05 e são separadas por um espaço no qual há vácuo. Se a superfície externa está a 280 K e a superfície interna está a 95 K, qual é a taxa mássica de perda de oxigênio devido à evaporação? (O calor latente de vaporização do oxigênio é de 2,13 × 105 J/kg.)
Passo 1
Vamos começar esquematizando o que o enunciado diz:
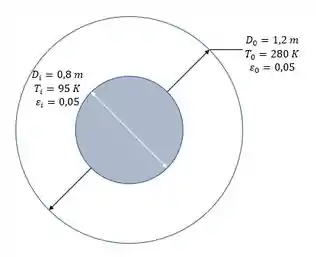
O enunciado também da pra a gente o calor latente de vaporização do oxigênio, ou seja, o quanto de calor que o oxigênio precisa receber pra mudar de fase:
Podemos usar a seguinte relação:
Temos uma esfera dentro da outa, então podemos usar a equação do livro:
Mas a transferência de calor acontece de fora, pra dentro, então !
Ficamos com:
Passo 2
Agora vamos ver o que mais falta para podermos achar
Sabendo que:
Temos:
é a área da esfera menor, que pode ser calulada:
Ficamos com:
Com , podemos substituir:
Calculando:
Aweeee!