Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 175

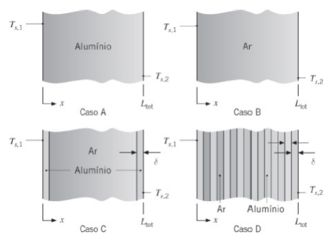
Determine o fluxo térmico condutivo através de várias camadas planas que estão submetidas a temperaturas nas extremidades de T s ,   1 = 301   K e T s ,   2 = 299   K , e encontram-se a pressão atmosférica. Sugestão: Não leve em conta os micro e nano efeitos no interior do sólido e suponha que o coeficiente de acomodação térmica para a interface alumínio–ar seja igual a a t = 0,92 .

  1. Caso A: A camada plana é alumínio. Determine o fluxo térmico q x " para L t o t = 600   μ m e L t o t = 600   n m .
  2. Caso B: A condução ocorre através de uma camada de ar. Determine o fluxo térmico q x " para L t o t = 600   μ m e L t o t = 600   n m .
  3. Caso C: A parede composta é formada por ar mantido entre duas folhas de alumínio. Determine o fluxo térmico para L t o t = 600   μ m (com a espessura da folha de alumínio igual a d = 40   μ m ) e L t o t = 600   n m (com a espessura da folha de alumínio igual a δ = 40   n m ).
  4. Caso D: A parede composta é formada por 7 camadas de ar retidas entre oito folhas de alumínio. Determine o fluxo térmico para L t o t = 600   μ m (com a espessura das folhas de alumínio e das camadas de ar iguais a δ = 40   μ m ) e L t o t = 600   n m (com a espessura das folhas de alumínio e das camadas de ar iguais a δ = 40   n m ).

Passo 1

Fala aí! Vamos resolver essa questão? Partiu!

O enunciado dá pra gente diferentes casos… Vamos analisar cada um com cuidado!

Mas antes de tudo precisamos de algumas informações adicionais que podemos buscar na tabela A.4, na tabela A.1 e na figura 2.8, beleza?

c p ,   a r = 1,007   J / k g . K k a r = 0,0263   W / ( m . K )

M a r = 28,97   k g / k m o l d a r = 0,372   .   10 - 9   m

k A l = 237   W / ( m . K )

Agora vamos para as continhas!

Na letra a, ele pediu pra gente o fluxo térmico, da camada de alumínio, apresentado dois valores de L , então vamos lá!

A gente sabe que a equação do fluxo térmico é dada por:

q x " = k   .   T s ,   1 - T s ,   2 L t o t

Primeiro para L t o t = 600   μ m :

q x " = 237   .   301 - 299 600   .   10 - 6

q x " = 7,9   .   10 5   W / m ²

Agora para L t o t = 600   n m :

q x " = 237   .   301 - 299 600   .   10 - 9

q x " = 7,9   .   10 8   W / m ²

Show!

Passo 2

Agora para a letra b, vamos fazer o mesmo que a letra, só que agora com a camada de ar, beleza?

Primeiro para L t o t = 600   μ m :

q x " = 0,0263   .   301 - 299 600   .   10 - 6

q x " = 87,7   W / m ²

Agora para L t o t = 600   n m :

q x " = 0,0263   .   301 - 299 600   .   10 - 9

q x " = 87700   W / m ²

Show de bola!

Passo 3

Partiu letra c! Também precisamos calcular o fluxo térmico, mas agora será um pouquinho diferente… Vamos lá!

Precisamos encontrar alguns termos para antes de ir para o cálculo que queremos, ok?

R = R M

R = 8,315 28,97

R = 0,287   k J / ( k g . K )

Vamos encontrar agora nosso c v :

c v = c p - R

c v = 1,007 - 0,287

c v = 0,720   k J / ( k g . K )

E o γ :

γ = c p c v

γ = 1,007 0,720

γ = 1,399

Tranquilo? Agora sim podemos ir encontrar o que nosso enunciado quer!

Passo 4

Primeiro com L t o t = 600   μ m → 600   .   10 - 6   m :

q = T s ,   1 - T s ,   2 R t ,   m - m + R t ,   m - s + R t ,   c o n d "

Precisamos do R t ,   m - m , vamos achar ele assim:

R t ,   m - m = L k a r

R t ,   m - m = L t o t - 2 . δ k a r

R t ,   m - m = 600   . 10 - 6 - 2   .   40   .   10 - 6 0,0263

R t ,   m - m = 0,0198   K . m ² / W

Agora o R t ,   m - s :

R t ,   m - s = λ m f p k a r   .   2 - a t a t . 9 . γ - 5 γ + 1

Opa! Precisamos encontrar esse λ m f p , vamos lá:

λ m f p = k B   .   T 2 . π . d ² . p

λ m f p = 1,381   .   10 - 23   .   300 2 . π . 0,372   .   10 - 9 ² . 1,0133   .   10 5

λ m f p = 66,5   .   10 - 9   m

Agora vamos colocar ele na equação anterior:

R t ,   m - s = 66,5   .   10 - 9 0,0263   .   2 - 0,92 0,92 . 9   .   1,399 - 5 1,399 + 1

R t ,   m - s = 9,39   .   10 - 6   K . m ² / W

Falta pouco! Precisamos agora do R t ,   c o n d " :

R t ,   c o n d " = 2 . δ k A l

R t ,   c o n d " = 2.40   .   10 - 6 237

R t ,   c o n d " = 3,38   .   10 - 7   K . m ² / W

Agora sim! Vamos achar a taxa de calor:

q = 301 - 299 0,0198   +   9,39   .   10 - 6   +   3,38   .   10 - 7

q = 101   W / m ²

Show!

Passo 5

Vamos fazer o mesmo agora para o L t o t = 600   n m → 600   .   10 - 9   m !

Precisamos do R t ,   m - m :

R t ,   m - m = L k a r

R t ,   m - m = L t o t - 2 . δ k a r

R t ,   m - m = 600   . 10 - 9 - 2   .   40   .   10 - 6 0,0263

R t ,   m - m = 1,98   .   10 - 6   K . m ² / W

O nosso R t ,   m - s será o mesmo, pois ele não depende de L , ok?

Vamos então para o R t ,   c o n d " :

R t ,   c o n d " = 2 . δ k A l

R t ,   c o n d " = 2.40   .   10 - 9 237

R t ,   c o n d " = 3,38   .   10 - 10   K . m ² / W

Arrasamos! Vamos achar a taxa de calor:

q = 301 - 299 1,98   .   10 - 6   +   9,39   .   10 - 6   +   3,38   .   10 - 10

q = 68,6   .   10 3   W / m ²

Conseguimos! Agora só falta a letra d!

Passo 6

Para a letra d vamos fazer o mesmo que na letra c, mas com as novas condições que ele deu, ok?

Primeiro com L t o t = 600   μ m → 600   .   10 - 6   m :

q = T s ,   1 - T s ,   2 R t ,   m - m + R t ,   m - s + R t ,   c o n d "

Precisamos do R t ,   m - m :

R t ,   m - m = L k a r

R t ,   m - m = L t o t   .   1 / 15 k a r

R t ,   m - m = 600   . 10 - 6 . 1 / 15   0,0263

R t ,   m - m = 0,00152   K . m ² / W

Novamente o nosso R t ,   m - s permanece o mesmo, ok?

Só precisamos agora do R t ,   c o n d " :

R t ,   c o n d " = 8 . δ k A l

R t ,   c o n d " = 8   .   40   .   10 - 6 237

R t ,   c o n d " = 1,35   .   10 - 6   K . m ² / W

Agora sim! Vamos achar a taxa de calor:

q = T s ,   1 - T s ,   2 7 .   R t ,   m - m + 7   .   R t ,   m - s + R t ,   c o n d "

q = 301 - 299 7   .   0,00152   +   7   .   9,39   .   10 - 6   +   1,35   .   10 - 6

q = 186,7   W / m ²

Tá quase…

Passo 7

Para a letra d vamos fazer o mesmo que na letra c, mas agora para o alumínio, ok?

Agora com o L t o t = 600   n m → 600   .   10 - 9   m :

Precisamos do R t ,   m - m :

R t ,   m - m = L k a r

R t ,   m - m = L t o t   .   1 / 15 k a r

R t ,   m - m = 600   . 10 - 9 . 1 / 15   0,0263

R t ,   m - m = 1,52   .   10 - 6   K . m ² / W

Só precisamos agora do R t ,   c o n d " :

R t ,   c o n d " = 8 . δ k A l

R t ,   c o n d " = 8   .   40   .   10 - 9 237

R t ,   c o n d " = 1,35   .   10 - 9   K . m ² / W

Agora sim! Vamos achar a última taxa de calor:

q = T s ,   1 - T s ,   2 7 .   R t ,   m - m + 7   .   R t ,   m - s + R t ,   c o n d "

q = 301 - 299 7   .   1,52   .   10 - 6   +   7   .   9,39   .   10 - 6   +   1,35   .   10 - 9

q = 26,2   .   10 3   W / m ²

Uhull! Terminamos!

Resposta

  1. Para L t o t = 600   μ m : q x " = 7,9   .   10 5   W / m ²

    2. Para L t o t = 600   n m : q x " = 7,9   .   10 8   W / m ²

  2. Para L t o t = 600   μ m : q x " = 87,7   W / m ²

    3. Para L t o t = 600   n m : q x " = 87700   W / m ²

  3. Para L t o t = 600   μ m : q x " = 101   W / m ²

    4. Para L t o t = 600   n m : q x " = 68,6   .   10 3   W / m ²

  4. Para L t o t = 600   μ m : q x " = 186,7   W / m ²

Para L t o t = 600   n m : q x " = 26,2   .   10 3   W / m ²

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

24 – Duas paredes espessas são separadas por uma lacuna de vácuo de espessura L. Um cilindro de diâmetro D, passa entre as paredes. Todas as superfícies são altamente polidas (suas emissividades são m
10 - A sensação de calafrio (resfriamento pelo vento), que é experimentada em dias frios com vento, está relacionada ao aumento da transferência de calor na pele humana exposta à atmosfera circundante
Considere uma parede composta que inclui um painel lateral em madeira dura com 8 mm de espessura; travessas de suporte em madeira dura com dimensões de 40 mm por 130 mm, afastadas com 0,65 m de distân
Vapor d’água a uma temperatura de 250°C escoa através de uma tubulação de aço (AISI 1010) com diâmetro interno de 60 mm e diâmetro externo de 75 mm. O coeficiente convectivo entre o vapor e a superfíc
Como uma alternativa para o armazenamento de materiais radioativos em águas oceânicas, propõe-se que o sistema do Problema 3.62 seja colocado em um grande tanque onde o escoamento de água, e assim o c