Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 2.Problemas - Ex. 57

Determine a pressão manométrica no interior de uma bolha de sabão de diâmetro (a) 0,2   c m e (b) 5   c m a 20   ° C .

Passo 1

A questão pede que a gente calcule a pressão manométrica P m a n do interior da bolha. A pressão manométrica é igual à pressão interna absoluta P i menos a pressão atmosférica P a t m . Como a pressão do lado de fora da bolha P e é igual à pressão atmosférica P a t m , a pressão manométrica P m a n é:

P m a n = P i - P a t m       ⟹       P m a n = P i - P e

Logo, calcular P i - P e é a mesma coisa que calcualr pressão manométrica P m a n , que o enunciado pede.

A equação 2 - 37 do livro é capaz de calcular essa diferença de pressão! Ela se encontra abaixo.

P i - P e = 4 ⋅ σ s R

onde σ s é a tensão superficial do sabão que forma a superfície da bolha e R é o raio da bolha.

No próximo passo, vamos aprender a encontrar o valor de σ s para calcular P i - P e .

Passo 2

A tensão superficial do sabão que está a 20   ° C se encontra na tabela 2 - 4 do livro.

σ s = 0,025   N m

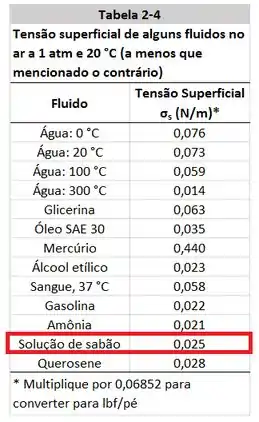
O raio R da bolha de sabão é a metade do diâmetro D que o enunciado informa.

R = D 2       ⟹         R = 0,2 2   c m       ⟹       R = 0,1   c m       ⟹       R = 0,001   m

Sabemdo de todos esses dados, nós podemos iniciar as contas.

Passo 3

Substituindo os dados na fórmula, encontramos:

P i - P e = 4 ⋅ σ s R       ⟹       P i - P e = 4 ⋅ 0,025 0,001       ⟹       P i - P e = 100   P a       ⟹       P m a n = 100   P a

Passo 4

O enunciado também pergunta qual é o valor de P m a n para uma bolha com um diâmetro D   de 5   c m . Nesse caso, o raio da bolha vale:

R = D 2       ⟹         R = 5 2   c m       ⟹       R = 2,5   c m       ⟹       R = 0,025   m

Logo, a pressão manométrica P m a n no interior da bolha vale:

P i - P e = 4 ⋅ σ s R       ⟹       P i - P e = 4 ⋅ 0,025 0,025       ⟹       P i - P e = 4   P a       ⟹       P m a n = 4   P a

Resposta

a   P m a n = 100   P a

b   P m a n = 4   P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Repita o cálculo da incerteza do Problema 1.40 para o ar em um balão de ar quente. Considere que a altura medida no barômetro é 759 mm de mercúrio com uma incerteza de ± 1 mm de mercúrio e a temperatu
Usando as dimensões nominais da lata de refrigerante dadas no Problema 1.47, determine a precisão com que o diâmetro e a altura devem ser medidos para que o volume da lata seja estimado dentro de uma
A massa da bola de golfe oficial americana é (45,4 ± 0,3 g) oz e o seu diâmetro médio é 43 ± 0,25 mm. Determine a massa específica e a densidade relativa da bola de golfe americana. Estime as incertez
As dimensões estimadas de uma lata de refrigerante são D = (66,0 ± 0,5) mm e H = (110 ± 0,5) mm. Meça as massas de uma lata cheia e de uma lata vazia, utilizando uma balança de cozinha ou de correio.
Do Apêndice A, a viscosidade μ (N · s/m2) da água à temperatura T (K) pode ser calculada a partir da equação μ = A × 10 B T - C , em que A = 2,414 × 10–5 N · s/m2, B = 247,8 K e C = 140 K. Determine a