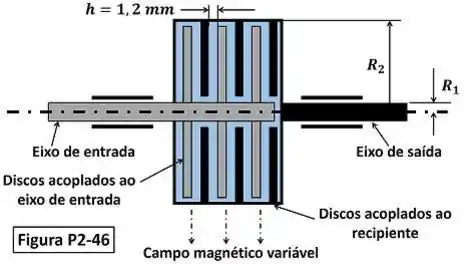
A viscosidade de alguns fluidos denominados fluidos magnetoreológicos (MR), muda quando é aplicado um campo magnético. Tais fluidos contem micropartículas magnetizáveis em suspensão num líquido transportador apropriado e são adequados para usar em embreagens hidráulicas controláveis. Veja a Figura P2-46. Os fluidos MR possuem viscosidades muito maiores do que os fluidos ER, e, frequentemente, exibem redutor de tensão no qual a viscosidade do fluido diminui à medida que a força de cisalhamento aumenta. Tal comportamento é também conhecido como comportamento pseudoplástico e é representado com sucesso pelo modelo caracteristico de Herschel-Bulkley expresso pela equação . Nessa expressão, é a tensão de cisalhamento aplicada, é tensão de escoamento, é o índice de consistência e é o indice de potencia. Para um fluido Herschel-Bulkley com , e , (a) determine uma relação para o torque transmitido por uma embreagem MR com discos acoplados ao eixo de entrada quando o eixo gira com velocidade angular enquanto o eixo de saída permanece estacionário e (b) calcule o torque transmitido por uma embreagem desse tipo com discos para , , e .
Passo 1
O enunciado pede que a gente calcule primeiro o torque que os discos acoplados ao eixo de entrada transmitem para os discos acoplados ao recipiente. Ou seja, os discos do eixo de entrada giram e fazem os discos do eixo de saída girar. No entanto, esses dois tipos de disco não estão diretamente ligados! Eles estão separados por um fluido viscoso.
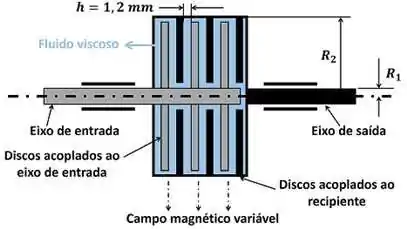
Isso quer dizer que o movimento dos discos de entrada é passado para os discos de saída através do movimento do fluido! Em outras palavras, os discos de entrada movem o fluido e esse fluido move os discos de saída. O fluido move o disco através da força de cisalhamento. O primeiro passo para calcular essa força é calcular o gradiente de velocidade do fluido. A figura abaixo mostra como a velocidade do fluido varia na direção dos eixos .
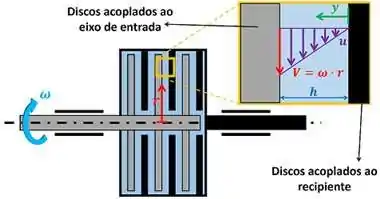
é a coordenada radial dos postos do disco. que varia do raio até o raio . é a velocidade de cada ponto dos discos cinzas acoplados ao eixo de entrada. é a velocidade angular dos discos acoplados ao eixo de entrada. Podemos considerar que a velocidade do fluido varia linearmente de (velocidade do disco preto) até (velocidade dos pontos do disco cinza). Dessa forma, pode ser calculado como:
Passo 2
Com essa informação e com a fórmula do enunciado, podemos calcular a tensão de cisalhamento que atua sobre o disco preto do eixo de saída.
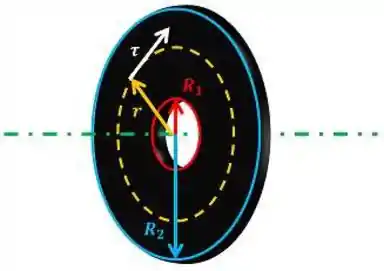
A figura abaixo mostra que essa tensão é a tensão aplicada a cada ponto dos discos do eixo de saída.
Passo 3
Agora, nós podemos calcular o torque aplicado sobre uma face do disco preto. O torque é a integral dos torques que são aplicados em cada pedacinho do disco.
O torque de cada pedacinho é igual à força cisalhante aplicada a cada pedacinho vezes o raio onde ela está sendo aplicada.
A força é igual à tensão de cisalhamento multiplicada pela área de cada pedacinho do disco.
A figura abaixo ilustra as variáveis , , e .
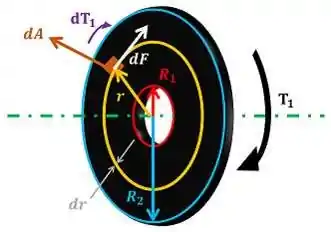
Substituindo na fórmula de e na fórmula de , encontramos:
Passo 4
é o torque aplicada a apenas uma face do disco. No tentanto, cada disco tem faces. Além disso, exitem discos! Isso quer dizer que o torque total é igual ao torque multiplicado pela quantidade total de faces .
Passo 5
Em segundo lugar, o exercício pede para a gente calcular o torque transmitido por uma embreagem desse tipo com discos para , , e . Mas antes de calcular , precisamos calcular a partir de pela fórmula abaixo.
Passo 6
Antes de usar a fórmula de , temos que converter , e de milímetro para metro .