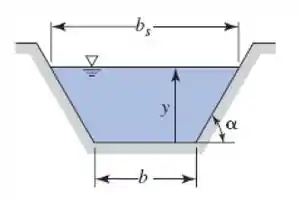
Determine a seção transversal da eficiência hidráulica ótima para um canal trapezoidal com inclinação lateral de 1 na vertical para 2 na horizontal se a descarga de projeto for 250 m³/s. A inclinação do canal é 0,001 e o fator de rugosidade de Manning é 0,020.
Passo 1
Beleza! Sabemos que a equação da descarga para o sistema é dada por:
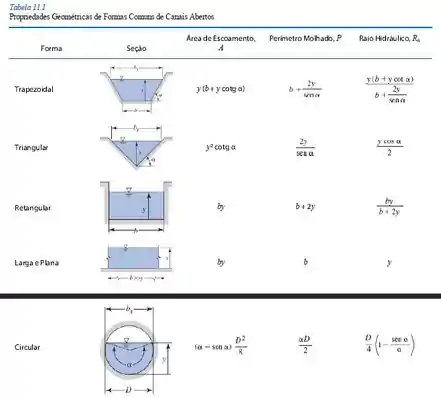
Então precisamos escrever a equação da descarga em função de , Com o auxílio da tabela de geometria fornecida nessa seção, temos:
Passo 2
Tá legal! Aqui vamos isolar da equação da área e substituir na do perímetro molhado, então, temos:
Então, substituindo na do perímetro molhado:
Agora, para obtermos a seção transversal da eficiência hidráulica ótima, vamos derivar a expressão anterior em relação à e depois igualar o resultado a zero para maximizar a eficiência em função de . Então, temos:
Para as condições ótimas então, devemos ter:
Então, substituindo esses valores na equação anterior, temos:
Passo 3
Agora vamos comparar a equação obtida para a área no passo 2 com aquela fornecida na tabela do passo 1, então, temos:
E, isolando a largura inferior do canal, temos:
Agora, vamos substituir esse valor na expressão para o raio hidráulico do passo 1, então, temos:
Como temos o mesmo termo dentro do parênteses no numerador e no denominador, então, podemos simplificar esse termo, ficando com:
Agora, antes de substituir os valores encontrados na expressão para a descarga, precisamos do valor de , que foi dado no enunciado, então, temos que:
E, os valores do coeficiente de rugosidade de Manning e da inclinação do fundo do canal foram dados no enunciado, de modo que:
Passo 4
Então, substituindo as expressões e valores encontrados na equação de descarga, temos:
Para resolver essa equação, precisamos do auxílio de uma calculadora, que nos dá:
E, com esse valor, podemos retornar à equação encontrada no passo 3 para a largura do fundo do canal:
E, substituir os valores conhecidos: