Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 68
O diagrama de Moody, Figura 6.13, é mais apropriado para determinar a perda de carga (ou quando Q, V, d, e L são conhecidos. Ele não é adequado para o segundo tipo de problema, ou seja, obter Q quando (ou ) é conhecido (veja o Exemplo 6.9). Prepare um diagrama de Moody modificado, cuja abscissa seja independente de Q e V, usando como parâmetro, do qual se pode ler imediatamente a ordenada para determinar Q ou V (adimensionais). Use seu diagrama para resolver o Exemplo 6.9.
Passo 1
E bora lá pra mais uma!
Cara, essa questão foi levantada analiticamente durante o capítulo, a expressão que nos fornece como parâmetro a perda de carga e não a taxa de fluxo é dada a seguir:
Assim, basta plotarmos para vários , assim, teremos algo da seguinte forma:
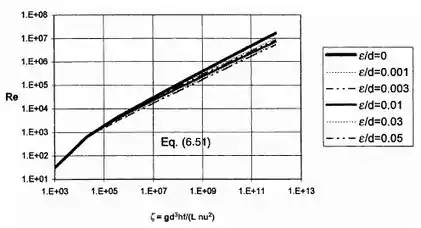
Onde cada curva é o valor de uma rugosidade relativa.
Passo 2
Analisando o Exemplo 6.9, teremos que, . Utilizando a expressão mencionada acima, encontraremos substituindo esses valores que:
Analisando o gráfico então, chegamos em um número de Reynolds entre 6E4
Substituindo nossos intervalos de Reynolds, chegaremos em:
Assim, teremos o seguinte intervalo de vazão:
Resposta
Ei, a resposta está no passo a passo :)