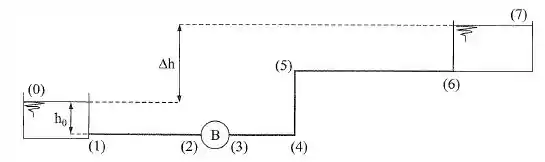
Na instalação da figura, deseja-se conhecer o desnível entre os dois reservatórios de água. Dados: potência fornecida ao fluido ; diâmetro ; ; .

Determinar também a rugosidade do conduto e a altura para que a pressão efetiva na entrada da bomba seja nula.

Começando pelo termo da carga da bomba, podemos escrever a potência da bomba como:

Agora vamos analisar o termo da perda de carga , como temos os coeficientes de perda localizada em cada um dos pontos, podemos escrever a perda de carga total como:

Agora precisamos encontrar a velocidade do escoamento, como temos a vazão e o diâmetro do tubo, ficou fácil:

Como o tubo é cilíndrico, temos , então, substituindo os valores conhecidos na equação para a perda de carga:

Agora podemos retornar à equação do desnível encontrada no passo 1:

Agora precisamos encontrar a rugosidade do conduto, para isso, vamos recorrer ao diagrama de Moody a seguir:

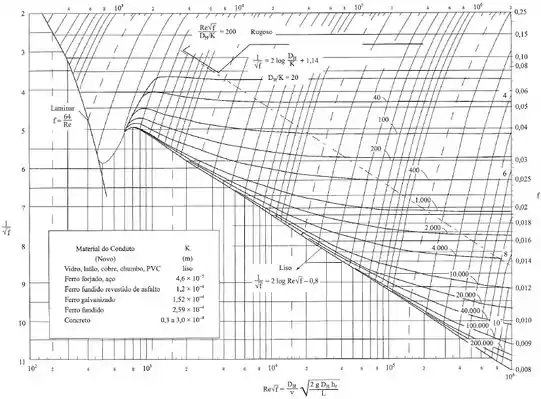
Como já temos a velocidade do escoamento, podemos calcular o número de Reynolds:

Com esse valor e com o fator de atrito dado no enunciado , cruzando essas informações no diagrama de Moody, interceptamos a curva para:

Isolando e substituindo o valor conhecido de temos:

Agora vamos aplicar o equilíbrio de energia entre os pontos 0 e 2:

Então, para que a pressão na entrada da bomba seja nula, devemos ter , reescrevendo a equação, temos:

Substituindo os valores conhecidos: