Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 43
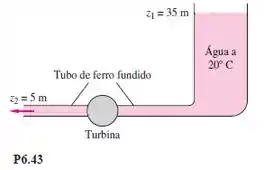
Um reservatório fornece água por 100 m de tubo de ferro fundido de 30 cm de diâmetro para uma turbina que extrai 80 hp do escoamento. Em seguida, a água descarrega na atmosfera. Despreze as perdas localizadas.
- Admitindo que , determine a vazão volumétrica (resultante de uma expressão polinomial cúbica). Explique por que existem duas soluções legítimas.
- Para um crédito extra, determine as vazões usando os fatores de atritos reais.
Passo 1
E lá vamos nóssssss! Bora lá pegar mais uma juntos!
Comecemos a nossa batalha! Primeiramente, vamos utilizar a equação de energia nisso aqui, bora lá:
Considerando um fluido incompressível, escoamento permanente e que , teremos:
Assim,
Tendo que, e que , temos:
Chegaremos em,
Passo 2
Chegamos na tão desejada equação cúbica, teremos então três raízes, sendo elas:
Galera, não temos velocidade negativa né?! Logo, apenas as duas positivas nos fazem sentido, ou seja, duas soluções legítimas. Assim,
As duas são válidas!
Passo 3
Para (b), vamos achar os fatores de atrito reais, assim:
Com a rugosidade relativa sendo, , pelo Diagrama de Moody, encontraremos que:
Utilizando esses fatores de atrito e utilizando na nossa equação de energia, da mesma forma como foi feita para a questão (a), chegaremos que:
Resposta
Ei, a resposta está no passo a passo :)