Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 169
Um dos módulos termoelétricos do Problema 3.13 está instalado entre um gás quente a e um gás frio a . O coeficiente convectivo associado ao escoamento dos dois gases é , enquanto a resistência elétrica da carga é de .
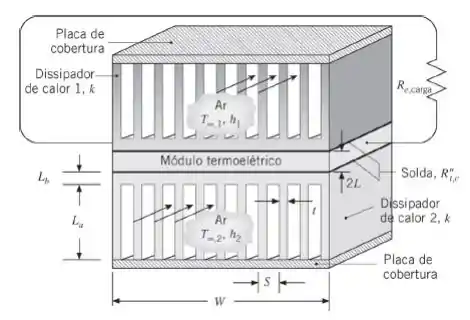
- Esboce o circuito térmico equivalente e determine a potência elétrica gerada pelo módulo para a situação, na qual, os gases quente e frio fornecem aquecimento e resfriamento convectivos diretamente para os módulos (sem dissipadores de calor).
- Dois dissipadores de calor (); veja no esboço), cada um com espessura da base e comprimento das aletas de , estão soldados nos lados superior e inferior do módulo. O espaço entre as aletas é de , enquanto as juntas de solda têm, cada uma, uma resistência térmica de . Cada dissipador tem aletas, de modo que e , como determinado a partir das exigências de que e . Esboce o circuito térmico equivalente e determine a potência elétrica gerada pelo módulo. Compare a potência elétrica gerada com a sua resposta para o item (a). Suponha extremidades adiabáticas nas aletas e coeficientes convectivos iguais aos da parte (a).
Passo 1
Fala aí! Temos duas letrinhas para responder… Vamos começar pela letra a!
Ela pede pra gente esboçar o circuito e depois determinar a potência elétrica gerada, show?
Vamos nessa!
Temos a imagem pra ajudar na montagem do circuito… Ele vai ficar com essa cara aqui olha:
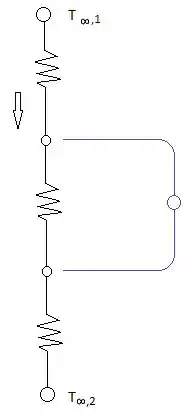
Agora vamos lembrar que pra calcular nossa potência podemos usar a fórmula:
Vamos então encontrar esse , beleza? Pra isso precisamos:
Agora precisaremos usar as equações 3.125 e 3.126 do livro… Tudo em prol da corrente, vamos lá:
Ops! Mas nós não temos e nem , vamos usar então a lei de resfriamento de Newton pra gente tentar montar um sistema pra descobrir o nosso .... Vamos lá:
Se a nossa energia produzida é igual a nossa energia dissipada, vamos ter que:
Passo 2
Agora podemos montar o que achamos em um sistema de três equações e três incógnitas, olha só:
Sistema a gente já está acostumado a resolver, né?
Resolvendo esse carinha aí vamos ter que:
Agora é só retornar lá na nossa equação da potência:
Agora partiu letra b!
Passo 3
A letra b, pede pra gente desenhar o novo circuito térmico e determinar novamente a potência elétrica…
Nosso circuito terá essa carinha aqui:
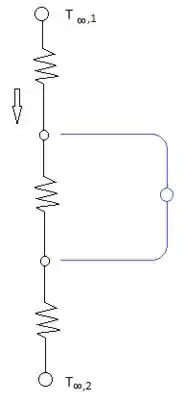
E novamente vamos precisar achar a corrente, mas dessa vez temos outros dados então faremos de um jeito diferente:
O único termo que tá faltando aí é o último, então vamos achar ele:
Vish! Temos esse pra encontrar também:
Agora vamos voltar ali em cima:
E voltando lá na equação da resistência total, temos:
Agora podemos usar as equações:
Agora vamos montar outro sisteminha, usando as mesma equações da letra a, beleza?
Resolvendo esse sistema vamos ter que:
E agora podemos calcular a potência:
Conseguimos! E chegamos a conclusão de que a nossa potência encontrada na letra b é 28 vezes maior que o anterior!