Distribuições de temperaturas no interior de uma série de paredes planas no instante inicial, no regime estacionário e em alguns tempos intermediários têm a forma mostrada na figura.

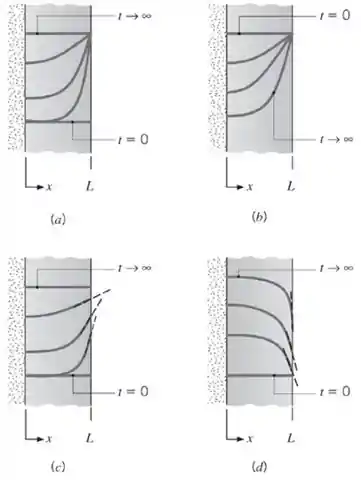
Para cada caso, escreva a forma apropriada da equação da difusão térmica. Também escreva as equações para as condições inicial e de contorno que são aplicadas em e . Se ocorrer geração volumétrica, ela é uniforme em toda a parede. As propriedades são constantes.

Para resolver essa questão vamos assumir que estamos com condução unidimensional, as propriedades são constantes e a radiação é desprezível.

A forma geral da equação do calor nas coordenadas cartesianas da constante para condução unidimensional é:

No estado estacionário essa equação resulta em:

Se não houver geração de energia térmica, a distribuição de temperatura no estado estacionário é linear (ou pode ser constante). E se houver geração uniforme de energia térmica, a distribuição de temperatura em estado estacionário deve ser parabólica.

No caso (a), a distribuição de temperatura no estado estacionário é constante. Então, não deve haver geração de energia térmica e a equação do calor é:

Como a temperatura inicial é uniforme em todo o sólido, a condição inicial é:

Em , a inclinação da distribuição de temperatura é zero o tempo todo, então, o fluxo de calor é zero (condição isolada) e a condição de contorno é:

Em , a temperatura é a mesma para todos os . Portanto, a temperatura da superfície é constante:

No caso (b), a distribuição de temperatura no estado estacionário não é linear e parece ser parabólica, então, há geração de energia térmica e a equação do calor é:

A temperatura inicial é uniforme, o gradiente de temperatura em é zero e a temperatura em é igual à temperatura inicial para todos os . Então, a condição inicial é:

E as condições de contorno são:

Com o lado esquerdo isolado e o lado direito mantido na temperatura inicial, a causa da temperatura decrescer deve-se a um valor negativo da geração de energia térmica.

No caso (c), a distribuição de temperatura no estado estacionário é constante, portanto, não há geração de energia térmica e a equação do calor é:

A temperatura inicial é uniforme em todo o sólido. Em , a inclinação da distribuição de temperatura é zero o tempo todo. Então, a condição inicial e a condição de contorno em são:

Em , nem a temperatura nem o gradiente de temperatura são constantes o tempo todo. Em vez disso, o gradiente de temperatura diminui com o tempo à medida que a temperatura se aproxima da temperatura de estado estacionário. Isso corresponde a uma condição de limite de transferência de calor por convecção. À medida que a temperatura da superfície se aproxima da temperatura do fluido, o fluxo de calor na superfície diminui. Então, a condição de contorno é:

A temperatura do fluido, deve ser maior que a temperatura da superfície inicial para fazer com que a temperatura da superfície aumente.

No caso (d), a distribuição de temperatura no estado estacionário não é linear e parece ser parabólica, então, há geração de energia térmica e a equação do calor é:

Como a temperatura está aumentando com o tempo, e não se deve à condução de calor devido a uma alta temperatura da superfície, a geração de energia deve ser positiva.

A temperatura inicial é uniforme e o gradiente de temperatura em é zero. A condição de contorno em é por convecção. O gradiente de temperatura e o fluxo de calor na superfície aumentam com o tempo, à medida que a geração de energia térmica faz com que a temperatura suba mais e mais acima da temperatura do fluido. Então, as condições iniciais e de contorno são: