Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 70

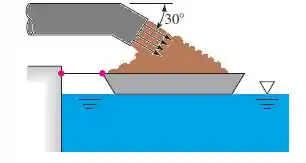
A draga da figura a seguir está carregando a barcaça com areia (d =2,6). A areia deixa o tubo da draga a 1,21 m/s com uma vazão em peso de 3781 N/s. Calcule a tensão no cabo de ancoragem causada por esse processo de carregamento.

Passo 1

Para calcularmos a tensão no cabo de ancoragem, precisamos entender que isso só será possível através de um balanço de forças, beleza? Mas pra isso, vamos precisar fazer um volume de controle adequado.

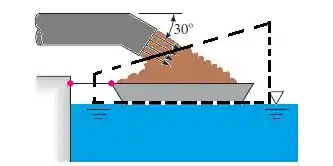
Aplicando o balanço de forças na direção x e precisamos lembrar que como temos uma velocidade de areia inclinada, precisamos decompor para obter o valor de sua componente x.

∑ F x = - T c a b o = - m ˙ a r e i a V a r e i a , x = - m ˙ a r e i a   V a r e i a c o s θ

Passo 2

Agora vamos substituir os paranauês, beleza? Precisamos lembrar sempre que foi dado pra gente a vazão em peso, então precisamos mudar isso aí pra nosso valor de vazão mássica.

m ˙ = P ˙ g = 3781 9,81 = 385,42   k g / s

T c a b o = 385,42   1,21   x   c o s 30 ° = 404   N

Resposta

T c a b o = 404   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O bocal horizontal da figura abaixo tem D 1 = 300m m e D 2 = 150m m , com pressão de entrada p 1 = 262k P a absoluta e V 2 = 17m / s . Para água a 20°C, calcule a força horizontal fornecida pelos para
O jato d’água da figura abaixo atinge a placa fixa na normal. Despreze a gravidade e o atrito e calcule a força F, em newtons, necessária para manter a placa fixa.
Água a 20°C escoa em regime permanente através da caixa abaixo, entrando na seção 1 a 2m/s. Calcule (a) a força horizontal e (b) a força vertical necessárias para manter a caixa parada contra o fluxo
Na figura abaixo, a pá fixa desvia o jato d’água em uma meia volta completa. Encontre uma expressão para a velocidade máxima do jato V 0 se a máxima força possível do suporte é F 0 .
Um líquido de massa específica ρ escoa através da contração brusca da figura abaixo e sai para a atmosfera. Considere condições uniformes ( ρ 1 , V 1 , D 1 ) na seção 1 e ( ρ 2 ,V 2 ,D 2 ) na seção 2.