Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 49
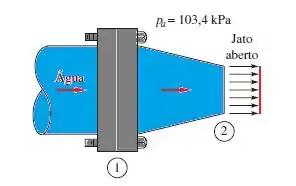
O bocal horizontal da figura abaixo tem e , com pressão de entrada absoluta e . Para água a 20°C, calcule a força horizontal fornecida pelos parafusos dos flanges para manter o bocal fixo.
Passo 1
Bora que bora para mais um desafio juntos?
Vamos lá, primeira coisa que precisamos fazer sempre é entender o problema físico! Então você vai concordar comigo que para um bocal aberto, !! Então vamos aplicar um volume de controle em volta do nosso bocal para analisarmos quais são as forças que estão atuando nele, show?
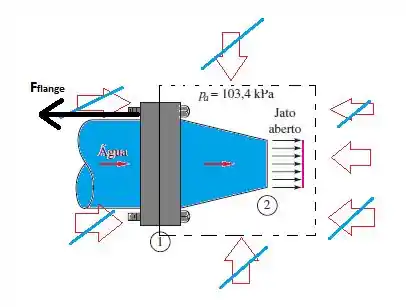
Você vai concordar comigo que a pressão atmosférica ela está atuando em todos os pontos do meu volume de controle, porém na área referente a saída do bocal, essas pressões não se cancelam!!
Vamos escrever nosso balanço de forças então!
Note que e são forças que estão se contrapondo por causa do nosso balanço de forças dentro do nosso volume de controle.
Passo 2
Sabemos que para um escoamento incompressível a vazão deve ser mantida dentro do nosso volume de controle, assim, podemos escrever o balanço de forças da seguinte forma:
Como conhecemos , bora escrever em função de ?
Lembre-se agora que, a força de pressão 1 está atuando na mesma área que a força de pressão atmosférica, então
Passo 3
Substituindo todos os valores dentro do nosso balanço de forças: