Um elemento de combustível nuclear, com espessura , é coberto com um revestimento de aço com espessura . O calor gerado no interior do combustível nuclear, a uma taxa , é removido por um fluido a , que se encontra em contato com uma das superfícies e é caracterizado por um coeficiente convectivo . A outra superfície encontra-se isolada termicamente. O combustível e o aço possuem condutividades térmicas e , respectivamente.
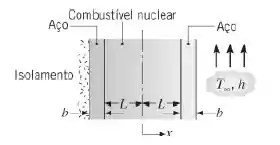
(a) Obtenha uma equação para a distribuição de temperaturas no combustível nuclear. Expresse seus resultados em termos de , , ,, , e .
(b) Esboce a distribuição de temperaturas para todo o sistema.
Passo 1
Fala galera!!
Nessa questão, queremos encontrar uma (a) expressão para a distribuição de temperatura no combustível, e a (b) forma de distribuição de temperatura para todo o sistema.
PRESSUPOSTOS:
(1) Transferência de calor unidimensional;
(2) Condições de estado estacionário;
(3) Geração uniforme;
(4) Propriedades constantes;
(5) Resistência de contato desprezível entre combustível e revestimento.
Passo 2
Podemos desenha o seguinte esquema para o combustível nuclear revestido de aço.
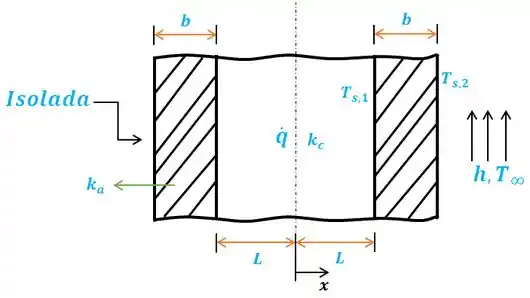
Passo 3
(a) Para resolver essa questão, podemos começar escrevendo Eq. 3.45 que é a solução geral para transferência de calor. Para o combustível temos o seguinte:
Aqui, é a temperatura na direção de , é a taxa de transferência de calor, é a condutividade térmica do combustível, é à distância na direção vertical e e são constantes arbitrárias.
Queremos encontrar e para isso, podemos usar as condições de contorno. A primeira condição se dá ao fato de que a superfície onde a parede está isolada, ou seja, podemos dizer que o fluxo de calor em é zero (para um balanço de energia aplicada a um volume de controle sobre a parede, ). Consequentemente:
Aplicando essa condição, temos o seguinte:
Agora vamos usar a segunda condição de contorno. Quando , temos que . Assim temos que:
Assim, temos que a equação de distribuição de temperatura é:
Passo 4
Queremos que a equação de distribuição de temperatura acima fique em função de e não em função de . Para isso, vamos usar o circuito de resistência térmica equivalente para o revestimento, como mostrado abaixo:
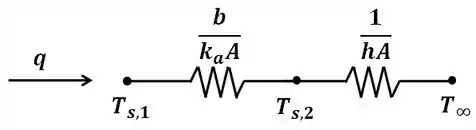
Temos que a quantidade de calor gerada no combustível é igual à taxa de calor conduzida. Ou seja:
Aqui, é a quantidade de calor gerado no combustível e é o volume.
Com o circuito térmico equivalente, podemos escrever a equação de condução de calor do combustível até a extremidade direita do revestimento. Assim temos:
Substituindo a taxa de calor conduzida, podemos encontrara temperatura da seguinte maneira:
Substituindo na equação de distribuição de temperatura encontrada no passo anterior, temos o seguinte:
Portanto, a distribuição de temperatura é:
Passo 5
(b) Para o período de , a taxa de transferência de calor é zero, e, portanto a temperatura é constante nesse período e igual a devido o gradiente de temperatura ser zero.
Para o período , o gráfico é parabólico e gradiente de temperatura aumenta com
Para o período de , o gradiente e uma constante, pois não a geração de energia, isso faz com que o gráfico seja uma reta.
Assim temos que o gráfico da distribuição de temperatura para todo o sistema se torne o seguinte:
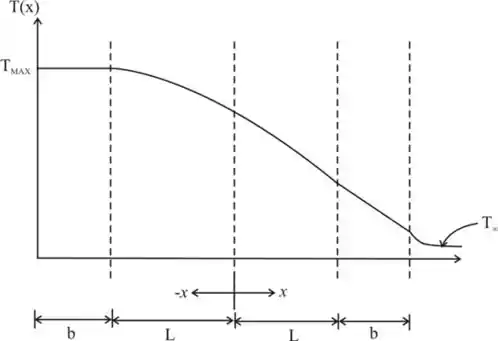
Resposta
(a)