Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 61

Um elemento de fluido bidimensional de dimensões d x e d y é transladado e distorcido como mostra a Figura P 4 - 60 durante o período de tempo infinitesimal d t = t 2 - t 1 . As componentes da velocidade no ponto P no instante inicial são u e v nas direções x e y , respectivamente. Considere o segmento da reta P A da Figura P 4 - 60 , e mostre que o módulo da taxa de deformação linear na direção x é

ε x x = ∂ u ∂ x

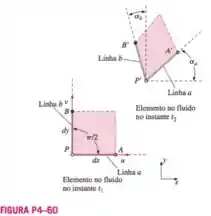
Passo 1

Bom, quando esse elemento é transladado, o ponto A acaba gerando uma distância e que ainda diminui o ângulo na linha a , ou seja, temos u + ∂ u ∂ x   d x d t para a direita e   v + ∂ v ∂ x   d x d t para cima. “Ah! Mas como assim d x ?” É porquê temos uma diminuição nos eixos em um instante de tempo, a derivada representa isso!

Visualmente, temos:

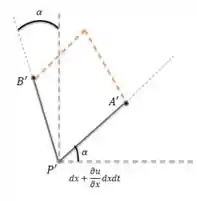
Portanto, no ponto final (que será representado por um P ' ), temos a seguinte localização do ponto A ' :

d x + ∂ u ∂ x   d x d t

Passo 2

Por definição, nós usamos os comprimentos encontrados, para calcularmos da seguinte maneira:

ε x x = ∂ ∂ x ( P ' A ' - P A P A )

O comprimento de P A nós já temos que é d x , substituindo

ε x x = d d t d x + ∂ u ∂ x   d x d t - d x d x = d d t ∂ u ∂ x d t = ∂ u ∂ x

Prontinho!!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o campo de velocidade estacionário, incompressível e bidimensional do Problema 4-55. Usando os resultados do Problema 4-55 ( a ) faça o seguinte: ( a ) Da definição fundamental de taxa de de
Um elemento de fluido bidimensional de dimensões d x e d y é translado e distorcido como mostra a Figura P4-60 durante o período de tempo infinitesimal d t = t 2 - t 1 . As componentes da velocidade n
Para o campo de velocidade do Problema 4-2, calcule a aceleração do fluido ao longo do eixo central do bocal como função de x e dos parâmetros dados.
Considere a visualização do escoamento em um cone de 12° na Figura P4-24C. Estamos vendo linhas de corrente, linhas de emissão, linhas de trajetória ou linhas de tempo? Explique.Visualização do escoam
Qual é a definição de uma linha de corrente? O que indicam as linhas de corrente?