Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 22
Qual é a definição de uma linha de corrente? O que indicam as linhas de corrente?
Passo 1
Uma linha de corrente é uma curva que é tangente em todos os pontos ao vetor velocidade . Por exemplo, imagine a água escoando ao longo de um rio. Considere que esse rio possui uma pedra que obriga a água a contorná-la para continuar o seu trajeto. Nesse caso os vetores de velocidade de cada ponto do rio seriam parecidos com os vetores abaixo.
A figura acima mostra a velocidade do fluido em cada ponto no mesmo instante . Por isso, essa figura é como se fosse uma foto da velocidade que registrou esse vetor em cada ponto marcado. A curva que for tangente as essas velocidades ao longo de todo o escoamento é chamada de linha de corrente. Podemos reconhecer duas linhas de corrente na figura acima!
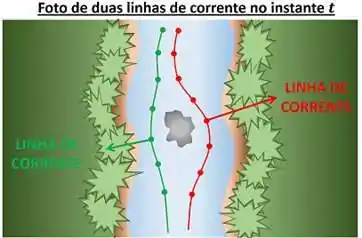
Podemos comparar a imagem acima com a imagem anterior e perceber que as linhas de corrente são tangentes aos velores de velocidade anteriores.
Passo 2
Como as linhas de corrente são tangentes ao vetor velocidade do fluido em um ponto, elas indicam a direção para onde cada partícula do fluido se move no escoamento em um instante . Ou seja, as linhas de corrente do rio mostram a direção de movimento de cada partícula do fluido em um mesmo instante!
Resposta
Uma linha de corrente é uma curva que é tangente em todos os pontos ao vetor velocidade local instantâneo . Ela indica a direção instantânea de movimento do fluido no escoamento.