Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 5.Problemas - Ex. 76
Uma embarcação de combate a incêndios deve trabalhar nas áreas costeiras retirando água do mar com uma densidade de por meio de um tubo com de diâmetro a uma vazão de e descarregando-a por meio do bocal de uma mangueira de diâmetro de saída de . A perda de carga irreversível total do sistema é de , e a posição do bocal está acima do nível do mar. Para uma eficiência de bomba de , determine a entrada necessária de potência de eixo na bomba e a velocidade de descarga de água.
Passo 1
Temos que determinar a potência necessária e a velocidade de saída, para a mangueira que esta operando no barco.
Como ele nos deu a densidade da água como utilizaremos claro está e também não mencionou o fator de correção de atrito, portanto, por convenção, teremos .
Para determinara a potência necessária tem que determinar primeiramente a carga útil que esta bomba está executando, por meio da equação do balanço energético.
Escolhendo dois pontos de referência (1) como a superfície do mar, (2) como a ponta da mangueira que está jorrando a água.
Como estes dois pontos se encontram na mesma pressão, pressão atmosférica, teremos .
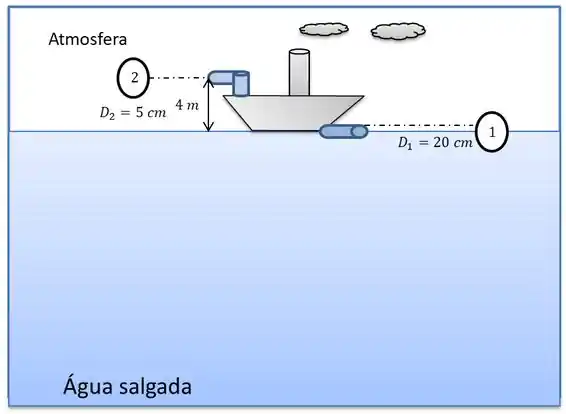
Temos um detalhe que, a velocidade , pois a velocidade é referente o quão rápido esvaziasse o tanque, como o nosso tanque é tão grande, como o oceano, esta velocidade referente comparada ao tanque é zero.
Passo 2
Para determinarmos a velocidade de saída é tranquilo, temos a vazão volumétrica da mangueira e o diâmetro da mangueira, dividindo estas duas grandezas teremos a velocidade:
Passo 3
Para determinar a carga útil feita pela bomba, temos que determinar pela equação do balanço energético:
Isolando a carga útil e simplificando oque é possível:
Substituindo os valores:
Passo 4
Agora que temos a carga útil da bomba, podemos determinar o potencial útil:
Substituindo valores:
Passo 5
Finalmente podemos determinar potência necessária:
Isolando e substituindo os valores: