Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 5.Problemas - Ex. 66
Uma bomba de 7hp (eixo) é usada para elevar a água até de altura. Se a eficiência mecânica da bomba for de determine a vazão de volume máxima da água.
Passo 1
Temos uma bomba especifica para elevar a água a e temos que determinar sua vazão.
Fazendo uma ilustração do que temos aqui:
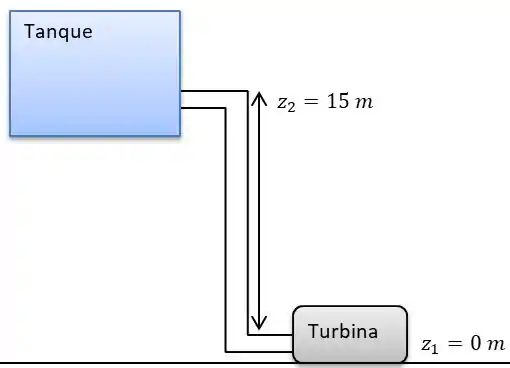
Bem simples eu sei, mas é suficiente para entendermos os próximos pontos que serão discutidos.
Assumindo que o fluxo é constante, água um fluido incompressível e não ocorrerá perdas por atrito, ou seja, .
Tendo a densidade da água como padrão .
Para dar início ao exercício temos que escolher dois pontos das superfícies, em que um deles será o ponto 1 como início da coluna de água, coordenada , e o ponto 2 o final da coluna de água, coordenada . Os dois pontos estarão abertos para atmosfera . A velocidade e serão iguais.
Passo 2
Levando em consideração oque foi escrito no passo 1, temos que a equação do balanço energético fica:
Simplificando em que, as pressões se anulam, as velocidades também se anularam, sobrando apenas a coluna necessária 2 e o trabalho da bomba.
Abrindo o fluxo de massa:
Determinamos o trabalho útil da bomba, mas desejamos a vazão da bomba, para isso, como enunciado nos deu o rendimento e o trabalho do eixo, podemos determinar .
Passo 3
Retomando a equação que determinamos no passo 2, temos:
Isolando a vazão: