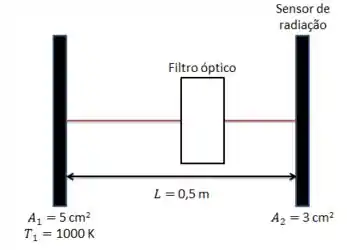
Uma pequena superfície de área 5 cm2 emite radiação como um corpo negro a 1000 K. Um sensor de radiação de área 3 cm2 é colocado na direção normal da visualização da superfície na distância . Um filtro óptico com a seguinte transmissividade espectral é colocado na frente do sensor:
Considerando que a distância entre o sensor de radiação e superfície é 0,5 m, determine a irradiação medida pelo sensor.
Passo 1
As informações que temos são: as áreas das superfícies 5cm2 e 3 cm2 e a temperatura da fonte 1.000 K. A fonte emite como um corpo negro, ou seja, emite radiação em todas as direções de forma uniforme. Também sabemos que a radiação passa um filtro, que tem um perfil de transmissividade:
O exercício nos pede para determinar a irradiação que chega no sensor.
Passo 2
Nosso primeiro passo é determinar o ângulo sólido. Vamos considerar que a radiação atinge a superfície 2 na direção normal, ou seja, o ângulo entre as superfícies é . Sabendo disso, o ângulo sólido é dado por:
Agora iremos calcular a potência transmitida pelo filtro. Como o filtro não transmite de maneira uniforme, teremos que integrar a potência em relação ao comprimento de onda. Tudo bem?
A potência transmitida pode ser calculada por:
Lembrando que usamos porque nossa fonte emite radiação como um corpo negro. Continuando:
Podemos aproximar utilizando a função de radiação do corpo negro :
Vamos usar isso para encontrar a potência transmitida:
Pela tabela 12-2 do capítulo do livro temos que para:
Então nossa potência fica:
Passo 3
Agora que encontramos a potência transmitida vamos determinar a intensidade da radiação:
Com a intensidade em mãos finalmente podemos determinar a irradiação que chega ao sensor:
Resposta
A irradiação que atinge o sensor é de .