Enunciado
Termodinâmica - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 9.Problemas - Ex. 84
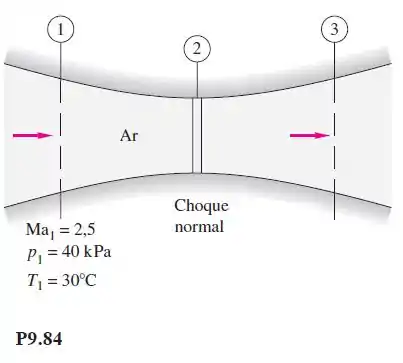
Ar escoa através de um duto como na Figura P9.84, em que A1 5 24 cm2, A2 5 18 cm2 e A3 5 32 cm2. Um choque normal se forma na seção 2. Calcule (a) a vazão em massa, (b) o número de Mach e (c) a pressão de estagnação na seção 3.
Passo 1
Bora pra mais uma!
Temos informações suficientes na seção 1 para calcular o fluxo de massa, da forma:
(a)
Daí, calculamos a vazão mássica:
Agora, mova isentropicamente de 1 para 2 a montante do choque, e, daí, para 3:
Aí, com a tabela B, lemos Então, conseguimos calcular a pressão através do choque:
(b) E então, o numero de Mach na seção 3, da forma:
Passo 2
(c) Por fim, obtemos a razão de pressão de estagnação em todo o choque:
Resposta
- 0,96kg/s
- 0,27
- 435kPa
Exercícios de Livros Relacionados
O ar comprimido de um grande tanque (Figura P9.32) escapa por um bocal a uma velocidade de saída de 235 m/s. O manômetro de mercúrio mede h = 30c m . Admitindo escoamento isentrópico, calcule a pressã
No Problema P3.34, ainda não sabíamos nada a respeito de escoamento compressível, e por isso adotamos meramente as condições de saída p 2eT 2 e calculamos V 2 como uma aplicação da equação da continui
Ar escoa isentropicamente por um duto de área variável. Na seção 1, A 1 = 20c m 2 ,p 1 = 300k P a ,ρ 1 = 1,75 k g m 3 ,eM a 1 = 0,25 . Na seção 2, a área é exatamente a mesma, mas o escoamento é bem m
Ar, nas condições de estagnação de 500 K e 200 kPa, escoa por um bocal. Na seção 1, em que a área é 12 cm2, a massa específica é 0,32 kg/m3. Admitindo escoamento isentrópico, (a) determine a vazão em
Uma força F = 1.100 N empurra um pistão de 12 cm de diâmetro através de um cilindro isolado contendo ar a 20oC, como na Figura P9.48. O diâmetro de saída é 3 mm e pa 5 1 atm. Calcule (a) Vs, (b) Vp e