Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 1.Exercício - Ex. 12

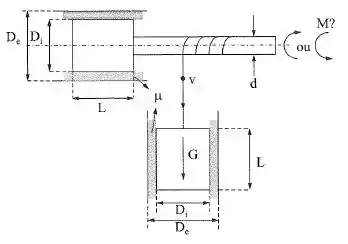
No sistema da figura, o corpo cilíndrico de peso G desce com velocidade constante v = 2   m / s , fazendo o eixo girar. Dados μ = 10 - 3   N ⋅ s / m 2 ; L = 2 / π   m ; D e = 50,2   c m ; D i = 50   c m ; d = 10   c m ; G = 50   N , qual é o momento aplicado por um agente externo no eixo? É motor ou resistente?

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O problema quer saber qual o momento externo deve ser aplicado para que o sistema fique em equilíbrio. Sabemos que o momento provocado por uma força externa, para o caso, é dado por:

M = F ⋅ d 2

Por isso devemos descobrir a força F que deve ser aplicada. Observe o diagrama de corpo livre abaixo:

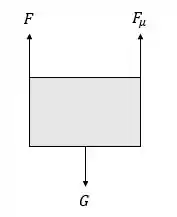
Temos que a condição de equilíbrio é dada por:

F + F μ = G

Onde F μ = τ ⋅ A , e representa a força causada pelas tensões de cisalhamento.

Passo 2

Agora vamos resolver a equação da condição de equilíbrio:

F + τ ⋅ A = G

Como sabemos que:

τ = μ d v d y

E:

A = π D L

Temos que:

F + μ d v d y ⋅ π D L = G

Substituindo os valores temos que:

F + 10 - 3 2 50,2   c m   - 50   c m 2 π 50   c m 2 π   = 50   N

Passo 3

Podemos encontrar uma relação para as velocidades a partir dos raios. Temos que:

u 2 = u 3 R 2 R 3

Resolvendo, temos que:

u 2 = 0,5 0,101 0,2

Sabemos também que:

u 1 = ∆ u + u 2

Substituindo os valores, temos que:

u 1 = 1,04 + 0,2525

u 1 = 1,29   m / s

Passo 4

Com estes valores, podemos utilizar a seguinte fórmula para encontrar a rotação.

n 1 = u 1 2 π R 1

Substituindo os valores, temos que:

n 1 = 1,29 2 π R 1

n 1 = 1,29 2 π 0,1 × 60

Logo:

n 1 = 123   r p m

Passo 5

O momento no eixo, é dado por:

M e i x o = τ A 1 R 1

Desenvolvendo, temos que:

M e i x o = μ ∆ u y 2 π R 1 L R 1

M e i x o = 2 π μ ∆ u y L R 1 2

Substituindo os valores, temos que:

M e i x o = 2 π 0,1 1,04 0,1 × 10 - 2 0,3 0,1 2

O momento provocado pelo fluido contra a rotação do eixo é de:

M e i x o = 2   N ⋅ m

Resposta

a )   n 1 = 123   r p m

b ) M e i x o = 2   N ⋅ m  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Umaaeronavesupersônicaviajaa2.700km/hemumaaltitudede27km.QualéonúmerodeMachdaaeronave?A que distância aproximada medida a partir da borda de ataque da asa da aeronave a camada-limite deve mudar de lam
Umaviãoestáemvoodecruzeiroaumaaltitudede5,5kmcomumavelocidadede700km/h.Conformeoaviãoaumentaa altitude,asuavelocidadeéajustadademodoqueonúmerodeMachpermaneçaconstante.Façaumesboçodavelocidadeemfunção
ÓleoSAE30a100ºCescoaatravésdeumtubodeaçoinoxidávelcom12mmdediâmetro. Qualéagravidadeespecíficaeo peso específicodoóleo?Seoóleodescarregadodotuboencheumcilindrograduadocom100mlem9segundos,oescoamentoél
O pistão da figura levanta, com velocidade constante, um peso G = 2000N sob a ação de uma pressão. Entre o pistão e o cilindro existe uma película de lubrificante ( ρ = 800k g / m 3 ; v = 10 - 5m 2 /
O dispositivo da figura gira a 1200r p m , acionado por um motor que mantém o torque constante, independentemente da rotação. Para variar a rotação, deloca-se o mancal móvel para a esquerda. Qual a no