Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 50
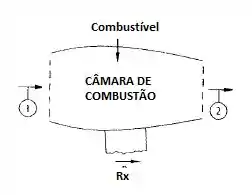
O motor a jato em uma bancada de testes, como mostrado abaixo, recebe ar a 20°C e 1 atm na seção 1, em que e . A relação combustível-ar é de 1:30. O ar sai pela seção 2, em que a pressão atmosférica, a temperatura é mais alta, e . Calcule a força horizontal de reação da bancada de testes, , necessária para manter o motor fixo.
Passo 1
E aí, preparado para mais um desafio de mecflu? Se sim ou se não, vem comigo que vamos encarar juntos!!
Primeira coisa que vamos lembrar aqui é, o enunciado nos deu velocidade e área da seção 1 e nos deu também a relação de combustível e ar, certo?
Bem, como temos um fluido incompressível, podemos dizer que sua densidade não varia dentro da câmara de combustão e por fim, , mas como calcular essa bendita densidade?
Vamos considerar um GÁS IDEAAAAALLL!
Lembrando que nossa temperatura deve estar em K e que , temos:
Passo 2
Aplicando um balanço de forças no nosso volume de controle em volta do nosso sistema mostrado abaixo!!
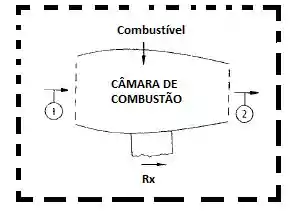
As forças de pressão se cancelam em volta do nosso volume de controle, restando apenas as forças que atuam por causa das vazões e a força Rx.
Passo 3
Como a vazão de combustível é 1/30 da do ar, podemos considerar ela próxima a zero, ou seja: