Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 106

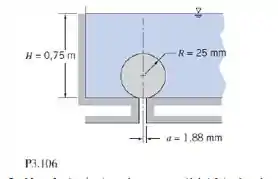
Uma esfera de raio 25   m m , feita de material de densidade específica S G   =   0,95 , está submersa em um tanque contendo água. A esfera é colocada sobre um furo de raio 1,88   m m , no fundo do tanque. Quando a esfera é solta, ela permanecerá no fundo do tanque ou flutuará para a superfície?

Passo 1

Para o problema, temos: dados da esfera e do fundo do tanque e devemos encontrar uma expressão para SG da esfera na qual flutuará para a superfície e um SG mínimo para permanecer em posição. Por isso, consideramos a água estática e incompressível e que a esfera é muito maior que o buraco no fundo do tanque.

Utilizamos as seguintes equações:

F e m p u x o = ρ g V , força de empuxo

∑ F y = 0 , somatório de forças no sentido de y

Passo 2

Segundo o diagrama de corpo livre, temos:

∑ F y = F L - F U + F B - W

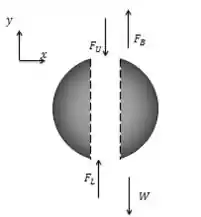
Onde:

F B = ρ g V n e t

F L = p a t m π a 2

W = S G ρ g V

V = 4 3 π R 3

V n e t = 4 3 π R 3 - π 2 a 2 R

Através dessas equações podemos obter:

F U = p a t m + ρ g H - 2 R π a 2

Agora, se a soma das forças verticais for positiva, a esfera flutuará para longe, enquanto que se a soma for zero ou negativa, a esfera permanecerá no fundo do tanque. Consequentemente:

∑ F y = p a t m π a 2 - p a t m + ρ g H - 2 R π a 2 + ρ g V n e t - S G ρ g V

= p a t m π a 2 - p a t m + ρ g H - 2 R π a 2 + ρ g 4 3 π R 3 - π 2 a 2 R - S G ρ g 4 3 π R 3

= p a t m π a 2 - p a t m + ρ g H - 2 R π a 2 + ρ g 4 3 π R 3 - π 2 a 2 R - S G ρ g 4 3 π R 3

Simplificando a expressão, temos

∑ F y = π g ρ 1 - S G 4 3 R 3 - H a 2  

∑ F y = π × 9,81 m s 2 × 999 k g m 3 1 - 0,95 4 3 ( 25 × 10 - 3 ) 3 - ( 0,75 ) ( 1,88 × 10 - 3 m ) 2

∑ F y = - 0,0495   N

Portanto, a esfera permanece no fundo do tanque!!

Resposta

∑ F y = - 0,0495   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As correntes oceânicas podem ser rastreadas por flutuadores Swallow [2], que receberam esse nome em homenagem ao Dr. John Swallow, do Reino Unido, que os projetou em 1955. Houve muitas alterações no p
Quando um peso de 22 N é colocado na extremidade de uma barra de madeira flutuante na Figura P2.119, a barra inclina a um ângulo theta com seu canto superior direito na superfície, como mostra a figur
Uma barra uniforme de madeira (d = 0,65) tem 10 cm por 10 cm por 3 m e está articulada em A, como mostra a Figura P2.120. A que ângulo theta a barra flutuará em água a 20°C?
Um malandro colocou óleo, de densidade do, no ramo esquerdo do manômetro da figura abaixo. Não obstante, o tubo em U ainda é útil como um dispositivo de medida de pressão. Ele é ligado a um reservatór
A solid sphere, of diameter 18 cm, fl oats in 208C waterwith 1527 cubic centimeters exposed above the surface.(a) What are the weight and specifi c gravity of this sphere?(b) Will it fl oat in 208C ga