Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas Abrangentes - Ex. 8

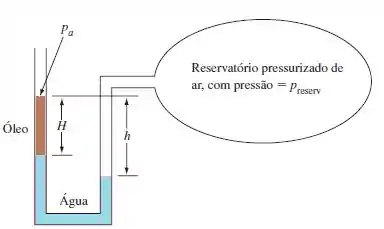
Um malandro colocou óleo, de densidade do, no ramo esquerdo do manômetro da figura abaixo. Não obstante, o tubo em U ainda é útil como um dispositivo de medida de pressão. Ele é ligado a um reservatório pressurizado, como na figura é mostrado. (a) Encontre uma expressão para h em função de H e outros parâmetros do problema. (b) Encontre o caso especial do seu resultado em (a) quando p r e s e r v = p a . (c) Admita que H = 50 cm, p a = 101,2   k P a , p r e s e r v seja 1,82 kPa mais alto do que p a e d0 = 0,85. Calcule h em cm, ignorando os efeitos de tensão superficial e desprezando os efeitos da densidade do ar.

Passo 1

Bora que bora para mais um problema pra gente resolver juntos?

Primeiro de tudo vamos escrever nossa equação de pressão no nível i do tubo.

p i = p a + ρ g H + ρ á g u a g h - H = p t a n q u e

ρ = d o ρ á g u a

Vamos ignorar a coluna de ar por enquanto, beleza?

Passo 2

(a) Resolvendo para h a nossa equação do passo 1, temos:

h = p t a n q u e - p a ρ á g u a g + H 1 - d o

Passo 3

(b) e (c) Quando temos p t a n q u e = p a :

h = H 1 - d o

Agora se formos usar os valores dados pra gente no enunciado para fazermos a letra (c), teremos que:

h = 1820 998 9,81 + 0,05 1 - 0,85 = 0,186 + 0,0075 = 0,193   m = 19,3   c m

Resposta

a h = p t a n q u e - p a ρ á g u a g + H 1 - d o

b h = H 1 - d o

c = 19,3   c m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma superfície submersa curva, no formato de um quarto de cilindro com raioR=0,3m está mostrada na figura. A forma pode resistir a uma carga máxima vertical de 1,6k N antes de se romper. A largura é w
Uma esfera de raio R está parcialmente imersa, a uma profundidade d, em um líquido com densidade relativa SG. Obtenha uma expressão algébrica para a força de empuxo atuando sobre a esfera como uma fun
Uma canoa é representada por um semicilindro circular reto, com R = 0,35m e L = 5,25m . A canoa flutua sozinha em água com seu fundo a uma profundidade d = 0,245m . Estabeleça uma expressão algébrica
Uma tora cilíndrica, com D = 0,3 m e L = 4 m, é mais pesada na sua extremidade inferior, de modo que flutua verticalmente com 3 m submersos na água. Quando deslocada verticalmente da sua posição de eq
Determine o peso específico da esfera mostrada na figura, se o seu volume é de 0,025m 3 . Enuncie todas as considerações feitas. Qual será a posição de equilíbrio da esfera, se o peso for removido?