Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 78

Esferas de 40   m m de diâmetro, aquecidas até uma temperatura uniforme de 400 ° C , são subitamente retiradas de um forno e colocadas em um banho de ar com escoamento forçado, operando a 25 ° C com um coeficiente convectivo de 300   W / ( m 2 · K ) na superfície das esferas. As propriedades termofísicas do material das esferas são ρ = 3000   k g / m 3 , c = 850 J k g · K   e k = 15   W / ( m · K ) .

(a) Quanto tempo as esferas devem permanecer no banho de ar para que 80% de sua energia térmica seja removida?

(b) As esferas são então colocadas em uma caixa de armazenamento que impede mais transferência de calor com o ambiente. Qual temperatura uniforme as esferas vão atingir após um longo tempo?

Passo 1

Vamos lá! Nosso problema nos pede o tempo necessário para a remoção de 80% da energia térmica da esfera, mas antes que tal desenharmos um esboço do comportamento desse problema pra entendermos o que o ocorre. Fica assim.

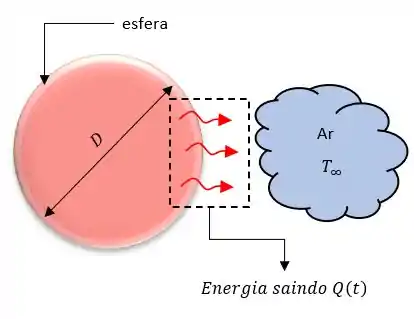
Agora vamos as nossas famosas considerações pra resolver nosso problema.

I - P r o p r i e d a d e s   c o n s t a n t e s

I I - T r a n s f e r e n c i a   d e   c a l o r   s o m e n t e   n o   s e n t i d o   r a d i a l

I I I - N ã o   h á   p e r c a   d e   t e m p e r a t u r a   n o   m e i o   t e m p o   d o   f o r n o   a t é   o   b a n h o   d e   a r

Passo 2

(a)

Para avaliarmos a porcentagem de energia removida precisamos da equação 5.55 , que nos diz que:

Q Q 0 = 1 - 3 θ 0 * ζ 1 3 sen ⁡ ( ζ 1 ) - ζ 1 cos ⁡ ζ 1

Lembrando que Q Q 0 = 0,8 .

Agora precisamos do número de B i o t que é:

B i = h r 0 k = 300 W m 2 ⋅ K ⋅ 0,02   m 15   W m ⋅ K = 0 , 4

Da tabela 5.1 temos:

C 1 = 1 ,   1164 ,   ζ 1 = 1,0528   r a d

Lembrando que da equação 5.53 , temos:

θ 0 * = C 1 e - ζ 1 2 F 0

Sendo F 0 = α t 0 r 0 2 , substituindo isso na equação 5.55 temos:

Q Q 0 = 1 - 3 C 1 e - ζ 1 2 α t 0 r 0 2 ζ 1 3 sen ⁡ ( ζ 1 ) - ζ 1 cos ⁡ ζ 1

Usando os valores encontrados temos:

0 , 2 = 3 ⋅ 1 ,   1164 ⋅ e - 1,0528   r a d 2   ⋅   5,88 ⋅ 10 - 6 t 0 0,02 2   1,0528   r a d 3

⋅ sen ⁡ 1,0528   r a d - 1,0528   r a d cos ⁡ 1,0528   r a d

Resolvendo pra t 0 temos que:

t 0 = 98,6   s e g u n d o s

Passo 3

(b)

Fazendo o balanço de energia das esferas temos:

E e n t r a - E s a i = Δ E = E f - E i

Sendo E f representando a energia da esfera pra t → ∞ .

E i = 1 - 0.8 Q 0 = 0,2 ρ V c T i - T ∞

E f = ρ V c T f - T ∞

ρ V c T f - T ∞ - 0,2 ρ V c T i - T ∞ = 0

T f = 0,2 ⋅ T i + 0,8 ⋅ T ∞

T f = 0,2 ⋅ 400 ° C + 0,8 ⋅ 25 ° C

T f = 100 ° C

Isso é tudo pessoal! Essa questão não é complicada, só precisamos estar atentos as considerações pra simplificar o máximo possível o balanço de energia!

Resposta

(a) t 0 = 98,6   s e g u n d o s

(b) T f = 100 ° C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

48. Com referência à ferramenta para processamento de semicondutores descrita no Problema 5.13, deseja-se, em algum ponto do ciclo de fabricação, resfriar o mandril, que é feito com liga de alumínio 2
55. Durante a operação transiente, o ejetor de um motor de foguete, feito em aço, não deve exceder uma temperatura máxima de operação de 1500 K quando exposto a gases de combustão caracterizados por u
50. Seja uma folha de acrílico com espessura L = 5 mm que é usada para cobrir um substrato metálico isotérmico e quente a Tq = 300°C. As propriedades do acrílico são ρ = 1990 kg/m3, cp = 1470 J/(kg ·
52. Aço é sequencialmente aquecido e resfriado (temperado) para aliviar estresses e torná-lo menos quebradiço. Seja uma placa com 100 mm de espessura (k = 45 W/(m · K), ρ = 7800 kg/m3, cp = 500 J/(kg
57. Em um processo de têmpera, uma lâmina de vidro que se encontra inicialmente a uma temperatura uniforme Ti é resfriada pela redução súbita da temperatura em ambas as superfícies para Ts. A lâmina t