Uma folha de cobre, com espessura , tem uma temperatura inicial de . Ela é subitamente imersa em água líquida, resultando em ebulição em suas duas superfícies. Para a ebulição, a lei do resfriamento de Newton é representada na forma , na qual é a temperatura da superfície do sólido e é a temperatura de saturação do fluido (neste caso ). O coeficiente de transferência de calor pode ser avaliado por . Determine o tempo necessário para a folha atingir uma temperatura de . Represente graficamente a temperatura do cobre versus o tempo para . No mesmo gráfico, represente o histórico da temperatura do cobre supondo que o coeficiente de transferência de calor seja constante, calculado na temperatura média do cobre . Suponha comportamento de capacitância global.
Passo 1
Vamos lá! Nosso problema nos pede a resistência térmica de contato, mas antes que tal desenharmos o comportamento desse problema pra entendermos o que o ocorre. Fica assim.
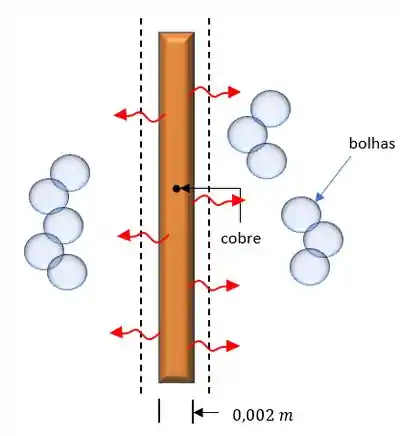
Agora vamos as nossas famosas considerações pra resolver nosso problema.
Passo 2
Vamos lá nosso problema nos pede o tempo necessário pra atingir a temperatura, , para isso vamos usar os dados da tabela para o cobre, a equação , sendo e e a equação assim nossa equação fica:
Organizando ambos os lados e integrando temos:
Substituindo os valores temos:
Passo 3
Vamos lá! como precisamos realizar o gráfico da temperatura ao longo do temos vamos usar a equação , que fica assim:
Substituindo os valores temos:
Como ele pede o gráfico pra duas situações, pra nosso , variando seguindo a equação e para um fixo para a temperatura assim:
Passo 4
Agora montando o gráfico para as duas equações temos:
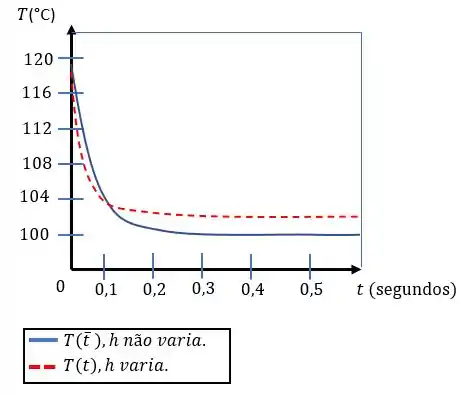
Vale a pena notar que o coeficiente de convecção começa muito alto e vai decaindo de acordo com a redução da diferença de temperatura entre a água e a folha de cobre, o que justifica a curva vermelha ser mais acentuada.
Isso é tudo pessoal!