Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 22

A parede plana de uma fornalha é fabricada em aço-carbono não ligado ( k   =   60   W / ( m   ·   K ) , ρ   =   7850   k g / m 3 ,   c   =   430   J / ( k g   ·   K ) ) e tem uma espessura L   =   10   m m . Para proteger essa parede dos efeitos corrosivos dos gases de combustão, uma superfície da parede é revestida por uma fina película cerâmica que, para uma unidade de área superficial, tem uma resistência térmica de R t , c ' ' =   0,01   m 2   ·   K / W . A superfície oposta encontra-se termicamente isolada da vizinhança.

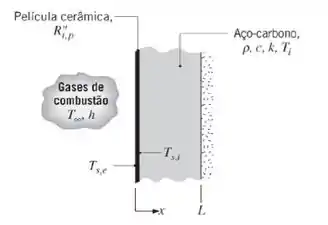
Na partida da fornalha, a parede se encontra a uma temperatura inicial de T i = 300   K e gases de combustão, a T ∞ = 1300   K , entram na fornalha, mantendo na película cerâmica um coeficiente convectivo h   =   25   W / ( m 2   ·   K ) . Supondo que a película tem uma capacitância térmica desprezível, quanto tempo irá levar até que a superfície interna do aço atinja uma temperatura de T s , i   =   1200   K ? Neste instante, qual é a temperatura T s , e na superfície externa da película cerâmica?

Passo 1

Okay galera, o negócio vai ficar quente, parecido com essa fornalha da questão hahahaha! O coeficiente global de transferência de calor da superfície do aço para o gás é

U = R t o t ' ' - 1 = 1 h + R f ' ' - 1 = 1 25 W / m 2 ⋅ K + 10 - 2 m 2 ⋅ K / W - 1 = 20   W / m 2 ⋅ K

Portanto,

B i = U L K = 20   W / m 2 ⋅ K   × 0.01   m 60   W / m   ⋅ K = 0.0033

E o método da capacitância por blocos pode ser usado, porque a temperatura no começo é constante, um sonho não?

Passo 2

Então, do método temos que:

T - T ∞ T i - T ∞ = e x p ⁡ ( - t / τ t ) = exp ⁡ - t R C = e x p   - U t / ρ L c

Isolando o tempo, e aplicando os valores que a questão nos dá:

t = - ρ L c U ln ⁡ T - T ∞ T i - T ∞ = - 7850 k g m 3 0.01 m 430 J k g ⋅ K 20 W m 2 ⋅ K ln ⁡ 1200 - 1300 300 - 1300

Para resolver esse monstro, da pra gente fazer numa calculadora cientifica! Temos então que:

t = 3 886   s = 1.08   h

Passo 3

Para acharmos a temperatura na superfície externa, vamos aplicar um equilíbrio de energia na superfície de fora!

h T ∞ - T s , o = T s , o - T s , i / R ' ' f

T s , o = h T ∞ + T s , i / R ' ' f h + ( 1 / R ' ' f )

Aplicando os valores que a questão nos da, temos que:

T s , o = 25 W m 2 ⋅ K × 1300 K + 1200 K 10 - 2 m 2 ⋅ K W 25 + 100 W m 2 ⋅ K  

T s , o = 1220   K

Resposta

t = 3886   s

T s , o = 1220   K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma lata de 10 cm de diâmetro interno e 30 cm de altura, cheia de água inicialmente a 25°C é colocada no refrigerador doméstico a 3°C. O coeficiente de transferência de calor na superfície da lata é d
Em um evento de erupção do vulcão, a lava encontrada fluindo no chão tem temperatura de 1200°C. O chão estava inicialmente a 15°C e o fluxo de lava possui um coeficiente de transferência de calor por
Duas hastes metálicas estão sendo aquecidas em um forno com temperatura uniforme de 1000°C e coeficiente de transferência de calor por convecção de 25 W m 2 K . A haste A é feita de alumínio ρ = 2702
Bolas de cobre ρ = 8933 k g m 3 ,k = 401 W m K ,c p = 385 J k g ° C ,α = 1,116 × 10 - 4 m 2 s inicialmente a 180°C são resfriadas no ar a 30 ° C por um período de 2 minutos. Considerando que as bolas
Um processo exotérmico ocorre de modo uniforme ao longo de uma esfera ( k = 300 W m K ,c p = 400 J k g . K ,ρ = 7500k g / m 3 ) de 10 cm de diâmetro, gerando calor a uma taxa constante de 1,2 M W m 3