Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 122

O teto plano do compartimento refrigerado de um caminhão para transporte de alimentos tem um comprimento L = 5 m e uma largura W = 2 m. Ele é fabricado com uma fina chapa metálica, à qual está fixada uma chapa de material isolante com espessura t = 25 mm e condutividade térmica k = 0,05 W/(m · K). Durante uma operação normal, o caminhão se move a uma velocidade V = 30 m/s em ar a T∞ = 27°C, com uma irradiação solar sobre a parte superior do teto de GS = 900 W/m2 e com a temperatura da superfície interna do teto mantida a Ts,i = –13°C.

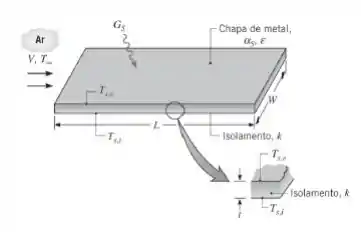
  1. O proprietário do caminhão tem a opção de selecionar um revestimento para o teto entre as três tintas que estão listadas na Tabela A.12 [Preto (Parsons), Branco (Acrílica), ou Branco (Óxido de Zinco)]. Qual deve ser a escolhida, e por quê?
  2. Com a tinta escolhida na parte (a), determine o valor da temperatura da superfície externa Ts,e em condições de regime estacionário. A camada-limite é perturbada na aresta frontal do teto, de tal forma que pode ser considerada a existência de escoamento turbulento ao longo de todo o teto. As propriedades do ar podem ser tomadas como sendo v = 15 × 10 –6 m2 /s, k = 0,026 W/(m · K) e Pr = 0,71.
  3. Qual é a carga (W) imposta ao sistema de refrigeração devido à transferência de calor através do teto?
  4. Explore o efeito da velocidade do caminhão sobre a temperatura da superfície externa e sobre a carga térmica.

Passo 1

Fala aí! Temos duas letrinhas para resolver… Mas antes de tudo precisaremos de uns dados a mais, podemos pegar eles na tabela A-4, usando um T s ,   s a i = 300   K :

v = 15   .   10 - 6   m ² / s k = 0,026   W / m . K

P r = 0,71

Beleza!

Vamos começar pela letra a, ok?

Ela quer que a gente escolha o revestimento para o teto entre parsons, acrílica e óxido de zinco…

Bom, vamos pensar: estamos buscando minimizar a transferência de calor, certo?

Então vamos minimizar a absorção solar, escolhendo o óxido de zinco! Pela tabela A.12, temos então:

ε = 0,93 α S = 0,16

Passo 2

Agora vamos para a letra b! Ela quer a temperatura da superfície externa, podemos achar fazendo um balanço de energia:

α S   .   G S   +   q c o n v "   -   E   -   q c o n d " = 0

α S   .   G S   +   h _   . T ∞ - T s ,   s a i   -   ε   .   σ   .   T s ,   s a i 4   -   k t   .   T s ,   s a i - T a ,   e n t = 0

Ops! Tá faltando gente aí, hein? Precisamos do h _ , vamos achar ele então!

h _ = N u _ L   .   k L

E podemos achar o N u _ L assim:

N u _ L = 0,037   .   R e L 4 / 5   .   P r 1 / 3

Ops! Ainda falta alguém… Vamos nele então:

R e L = V   .   L v

R e L = 30   .   5 15   .   10 - 6

R e L = 10 7

Agora sim, vamos voltar ali em cima:

N u _ L = 0,037   .   10 7 4 / 5   .   0,71 1 / 3

N u _ L = 13141

Aeee, vamos agora achar o h _ :

h _ = 13141   .   0,026 5

h _ = 68,3   W / m ² . K

E finalmente teremos a nossa temperatura:

0,16   .   900   +   68,3   . 300 - T s ,   s a i   -   0,93   .   5,67   .   10 - 8   .   T s ,   s a i 4   -   0,026 0,025   .   T s ,   s a i - 260 = 0

T s a i = 295,2   K

Show! Agora só falta a letra c!

Passo 3

Bom, na letra c precisamos encontrar a taxa de transferência de calor, vamos nessa!

q = k   .   A s t   .   T s ,   s a i - T s ,   e n t

q = 0,05   .   10 0,025   .   295,2 - 260

q = 704   W

Uhull! Arrasamos!

Resposta

  1. Óxido de zinco.

  2. T s a i = 295,2   K .

  3. q = 704   W .

  4. Depende do uso de software.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A absortividade espectral do alumínio revestido por uma fina camada de dióxido de silício pode ser aproximada por αλ,1 = 0,98 para λ Determine a temperatura de equilíbrio de uma peça plana do alumínio
Nossos alunos efetuam um experimento de laboratório para determinar a transferência de massa em uma toalha de papel embebida em água, na qual há convecção forçada e irradiação de lâmpadas radiantes. P
Uma toalha molhada está pendurada em uma corda de roupas sob condições nas quais uma superfície recebe irradiação solar de GS = 900 W/m2 e as duas superfícies estão expostas à radiação da atmosfera (c
Uma aleta anular com espessura t é usada como um radiador para dissipar calor de um sistema de potência espacial. A aleta tem sua parte inferior termicamente isolada e pode estar exposta à irradiação
Considere as condições de céu claro para as quais a radiação direta incide em θ = 30 ° , com um fluxo total (com base em uma área que é normal aos raios) o q d i r ' ' = 1000W / m 2 , e a intensidade