Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 11.Problemas - Ex. 101

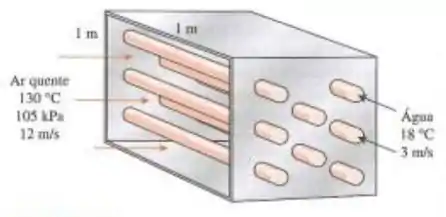
Um trocador de calor de escoamento cruzado é composto de 80 tubos de parede fina de 3 cm de diâmetro localizados em um duto de 1   m × 1   m   de seção transversal. Não há aletas fixadas nos tubos. A água fria c p = 4180 J k g . K entra nos tubos a 18°C com uma velocidade média de 3 m/s, enquanto o ar quente c p = 1010 J k g . K   entra no canal a 130°C e 105 kPa a uma velocidade média de 12 m/s. Considerando que o coeficiente global de transferência de calor é 130 W m 2 K , determine as temperaturas de saída de ambos os fluidos e a taxa de transferência de calor.

Passo 1

Bora continuar??

Para achar a taxa de transferência de calor nós vamos usar a seguinte relação:

Q ˙ = ε Q m a x ˙

Vamos começar calculando o valor máximo de transferência de calor:

Q m a x ˙ = C m i n T q ,   e n t r a - T f ,   e n t r a

Se a temperatura nós já temos:

T q ,   e n t r a = 130 ° C

T f ,   e n t r a = 18 ° C

Então nós só precisamos do C m i n . Lembrando que:

C = m ˙ c p

Para saber qual é o mínimo nós vamos calcular para o ar e para a água:

C q = m a r ˙ c p , a r

C f = m a g u a ˙ c p , a g u a

Sabendo que:

c p , a g u a = 4180   J k g . K

c p , a r = 1010 J k g . K

Conseguimos calcular agora?

Que nada né!! Precisamos da vazão mássica!! Se lembram da fórmula?

m a g u a ˙ = ρ á g u a V á g u a A c

m a r ˙ = ρ a r V a r ( A - A c )

Se lembrem que usamos essa área porque o ar está no exterior dos tubos!!

Como temos uma seção circular:

A c = n π D ² 4

Então:

m a g u a ˙ = ρ á g u a V á g u a n π D ² 4

m a r ˙ = ρ a r V a r A - n π D ² 4

Agora vamos ver nossos dados?

ρ á g u a = 1000 k g m 3

V á g u a = 3 m s

V a r = 12 m s

n = 80   t u b o s

D = 3 c m = 0,03   m

Vamos começar calculando a vazão mássica para a água, já que para ela nós temos todos os dados:

m a g u a ˙ = 1000 k g m 3 3 m s π × 80 × 0,03   m ² 4

m a g u a ˙ = 169,64 k g s

E como faremos para calcular a densidade do ar?

Fácil !! Basta usarmos:

ρ a r = P R T

Como:

P = 105   k P a

R = 0,287   k P a . m 3 k g . K

T = 130 ° C + 273 = 403   K

Sendo assim:

ρ a r = 105   k P a 0,287   k P a . m 3 k g . K 403   K = 0,9078 k g m 3

E agora a vazão mássica:

m a r ˙ = 0,9078 k g m 3 12 m s 1 m × 1 m - π × 80 × 0,03   m ² 4

m a r ˙ = 10,277 k g s

Passo 2

Agora que temos tudo o que precisamos podemos calcular os valores de C:

C q = m a r ˙ c p , a r = 10,277 k g s 1010 J k g . K = 10379,77 J s . K = 10379,77   W K

C f = m a g u a ˙ c p , a g u a = 169,64 k g s 4180 J k g . K = 709095,2 J s . K = 709095,2   W K

Sendo assim:

C m i n = C q = 10379,77   W K

C m a x = C f = 709095,2   W K

Calculando Q m a x ˙ :

Q m a x ˙ = 10379,77   W K 13 0 ° C - 18 ° C

Q m a x ˙ = 1162534,24   W

Passo 3

O próximo passo é calcular a eficácia, ok?

Para este trocador de calor:

ε = 1 - e - 1 C × 1 - e - N T U × C

Vamos começar calculando C:

C = C m i n C m a x

Substituindo:

C = 10379,77   W K 709095,2   W K = 0 , 0146

Animados para começar o NTU?

Lembrando que ele é dado por:

N T U = U A s C m i n

E que para tubos:

A s = n π D L

Substituindo nossos dados:

N T U = π 130 W m 2 K 80 0,03   m 1   m 10379,77   W K = 0,0944

Na fórmula da eficácia:

ε = 1 - e - 1 0,0146 × 1 - e - 0,0944 × 0,0146

ε = 0,09

Passo 4

Colocando na fórmula do Passo 1:

Q ˙ = 0 , 09 1162534,24   W

Q ˙ = 104628,07   W

Ou melhor:

Q ˙ = 10 4 , 62 8   k W

E achamos a primeira resposta !!

Bora pra segunda??

Passo 5

Bom galera, agora nós precisamos achar as temperaturas de saída !!

Para isso vamos usar a taxa de transferencia de calor que já achamos com relação às temperaturas de entrada e saída:

Q ˙ = C q T q ,   e n t r a - T q , s a i

Substituindo:

104628,07   W = 10379,77   W K 130 0 ° C - T q , s a i

T q , s a i = 119,92   ° C

Então:

T a r ,   s a í d a = 119,92   ° C

Agora nós vamos fazer a mesma para a glicerina, o fluido frio:

Q ˙ = C f T f , s a i - T f ,   e n t r a

Substituindo:

104628,07   W = 709095,2   W K T f , s a i - 18 ° C

T f , s a i = 18,147   ° C

Então:

T á g u a ,       s a í d a = 18,147   ° C

Gostaram dessa ?!

Resposta

  1. Q ˙ = 104,628   k W ;
  2. T a r ,   s a í d a = 119,92   ° C       |         T á g u a ,       s a í d a = 18,147   ° C .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um recuperador é um trocador de calor que aquece o ar usado em um processo de combustão pela extração de energia dos produtos de combustão (o gás de exaustão). Considere a utilização de um trocador de
Um trocador de calor casco e tubos, com um passe no casco e 20 passes nos tubos, utiliza água quente no lado dos tubos para aquecer óleo que escoa pelo lado do casco. O único tubo, de cobre, tem diâme
O dissipador de calor do Problema 7.29 tem sua utilização cogitada em uma aplicação na qual a dissipação de potência é de somente 70W e o engenheiro propõe o uso no resfriamento de ar a T ∞=20 ° C . L
Considere a operação do sistema forno-recuperador do Problema 11.60 sob condições nas quais energia química é convertida em energia térmica no combustor a uma taxa de q c o m b = 2,0 ⋅ 10 6W e energia
Resolva o Problema 8.109 a usando o método da efetividade ( ε – N U T ) .