Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 2.Exercício - Ex. 32

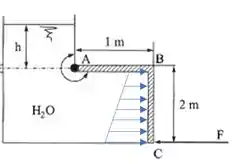
No esquema da figura, determinar a altura h e a mínima força F para que a comporta A B C permaneça em equilíbrio. Dados: largura = 1,5   m ; γ H g = 136000   N / m 3 ; γ H 2 O = 10000   N / m 3 .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Primeiramente, podemos aplicar a equação manométrica para descobrir h . Temos que:

P a t m + 0,25 γ H g - 0,4 + h γ á g u a = P a t m

Portanto:

0,25 γ H g = 0,4 + h γ á g u a

0,25 136000 = 0,4 + h 10000

10000 h = 34000 - 4000

h = 30000 10000

A altura h , será:

h = 3   m

Passo 2

Para descobrir a força mínima F para que a comporta permaneça em equilíbrio, vamos analisar as forças que agem na comporta. Observe o diagrama:

Essas forças F v e F H , podem ser calculadas a partir dos seus respectivos volumes de prisma pressão:

F v = γ h 1,5 1

F v = 10000 ( 3 ) 1,5 1

F v = 45000   N

E:

F H = 10000 5 + 10000 ( 3 ) 2 1,5 2

F H = 40000 1,5 2

F H = 12 0000   N

Passo 3

Também temos que encontrar o centro de aplicação da força horizontal para podermos aplicar o somatório de momentos e descobrir F . Temos que:

A equação do centro de pressão é dada por:

y C P = y C G + I C G y C G A

Temos que:

y C G = h + 2 2

y C G = 3 + 1 = 4   m

Temos também que:

I C G = b h 3 12 = 1,5 2 3 12

I C G = 1   m 4

E:

A = b h = 1,5 2

A = 3   m 2

Portanto:

y C P = 4 + 1 4 3

y C P = 49 12   m

Passo 4

A distância da força horizontal até o ponto A é de:

3 - 49 12 = 13 12

Aplicando o somatório de momento em A , temos que:

F H 13 12 + F v 0,5 = F 2

2 F = 12 0000 13 12 + 45000 0,5

F = 152 500 2

A força necessária para que o sistema permaneça em equilíbrio é de:

F = 762 50   N

Resposta

h = 3   m

F = 76250   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A comporta retangular de 200k g e 5m de largura mostrada na figura P 3 - 118 tem dobradiças em B e se inclina contra o piso em A , formando um ângulo de 45 ° com a horizontal. A comporta deve ser aber
A água de um reservatório com 25m de profundidade mantida no seu interior por uma parede com 150m de largura cuja seção transversal é um triângulo equilátero, como mostra a Figura P3-123. Determine (a
Um tubo em U contém água no braço direito e outro líquido no braço esquerdo. Observa-se que, quando o tubo em U gira a 30r p m em torno do eixo que está a 15c m do braço direito e 5c m do braço esquer
Um cilindro vertical com 1m de diâmetro e 2m de altura preenchido completamente com gasolina, cuja densidade é de740k g / m 3 . O tanque agora é posto a rodar em torno do seu eixo vertical a uma taxa
Repita o problema 3-106 para uma leitura de pressão manométrica de 240 k P a .