Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 2.Exercício - Ex. 49
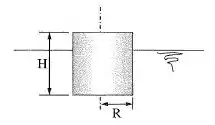
Qual a máxima altura de um cilindro de seção circular de raio , para que possa flutuar em equilíbrio estável com seu eixo na vertical em qualquer líquido? Dados: cilindro ; líquido .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Como o corpo está flutuando em equilíbrio, temos que o empuxo é igual ao peso:
Portanto, descobrimos uma relação entre a altura total do cilindro e sua altura submersa:
Passo 2
A condição de equilíbrio do corpo estável é de que:
Como:
Temos que:
O tamanho diz respeito a diferença de altura entre o centro de gravidade e o centro de pressão, logo:
Substituindo a relação do Passo , temos que:
Passo 3
Desenvolvendo a equação , temos que:
Logo:
Resposta
Exercícios de Livros Relacionados
Um cone circular reto sólido tem d = 0,99 e flutua verticalmente como na Figura P2.132. Essa é uma posição estável para o cone?
Considere um cilindro de densidade d1 flutuando verticalmente na água ( d = 1 ) , como na Figura P2.127. Deduza uma fórmula para os valores estáveis de D / L em função de d e aplique-a ao caso D / L =
Um bloco uniforme de aço ( d = 7,85 ) “flutuará” em uma interface mercúrio-água, como mostra a Figura P2.122. Qual é a razão entre as distâncias a e b para essa condição?
A barra uniforme da Figura P2.121, de tamanho L por h por b e com o peso específico γ b , flutua exatamente em sua diagonal quando uma esfera uniforme pesada é presa ao canto esquerdo, como mostra a f
Considere um cone circular reto uniforme de densidade d1 , flutuando com seu vértice para baixo na água ( d = 1 ) . O raio da base é R e a altura do cone é H . Calcule e coloque em gráfico a estabilid