Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 96
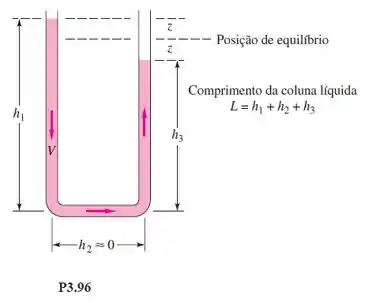
Estenda o Problema P3.90 par ao caso do movimento de um líquido em um tubo U, sem atrito, cuja coluna líquida é deslocada a uma distância Z para cima e então liberada, como na Figura P3.96. Despreze o curto trecho horizontal e combine as análises de volume de controle para os ramos da esquerda e da direita, deduzindo uma equação diferencial única para da coluna líquida.
Passo 1
Bora pra essa!
Bora fazer uma análise de movimento ai, primeiro começaremos pela perna da esquerda, assim:
Da perna da direita, teremos:
Ao somarmos as duas, o termo de pressão vai sumir, substituiremos as alturas da seguinte forma:
Passo 2
Olha só, se a gente fizer:
Vamos chegar em:
Se a gente resolver essa equação diferencial, vamos chegar em uma oscilação harmônica simples, olha:
Resposta
Ei, a resposta está no passo a passo :)